
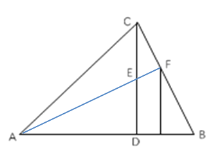
【题目】在△ABC中,CD⊥AB于点D,DA=DC=4,DB=2,AF⊥BC于点F,交DC于点E.
(1)求线段AE的长;
(2)若点G是AC的中点,点M是线段CD上一动点,连结GM,过点G作GN⊥GM交直线AB于点N,记△CGM的面积为S1,△AGN的面积为S2.在点M的运动过程中,试探究:S1与S2的数量关系
【答案】(1)![]() ;(2)S1+S2=4,见解析
;(2)S1+S2=4,见解析
【解析】
(1)先证明△ADE≌△CDB,得到DE=DB=2,在Rt△ADE中,利用勾股定理求出AE.
(2)过点G作CD,DA的垂直线,垂足分别为P,Q,证明△MGP≌△NGQ,所以S1+S2=S△AGQ+S△CGP= S△ACD-S四边形GQDP,即可求解.
(1)在△ABC中,CD⊥AB,AF⊥BC
∴∠ADC=∠AFB=90°
∵∠AED=∠CEF
∴∠EAD=∠BCD
在△ADE和△CDB中
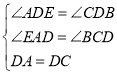
∴△ADE≌△CDB
∴DE=DB=2
∴AE=![]()
(2)在△ABC中,CD⊥AB,DA=DC=4,
点G是AC的中点
过点G作CD,DA的垂直线,垂足分别为P,Q.

则,GP=GQ=![]() DA=2
DA=2
∠PGQ=90°=∠GQN=∠GPM
∵GN⊥GM
∴∠MGN=90°
∴∠MGP=∠NGQ
∴△MGP≌△NGQ
S1+S2=S△AGQ+S△CGP= S△ACD-S四边形GQDP=![]()
故答案为:4


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,再解答问题:
已知在平面内有两点![]() ,
,![]() ,其两点间的距离公式为
,其两点间的距离公式为![]() ;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为![]() 或
或![]() .
.
(1)已知点A(2,4),B(-2,1),则AB=__________;
(2)已知点C,D在平行于y轴的直线上,点C的纵坐标为4,点D的纵坐标为-2,则CD=__________;
(3)已知点P(3,1)和(1)中的点A,B,判断线段PA,PB,AB中哪两条线段的长是相等的?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
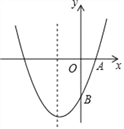
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、
B(0,﹣3)两点.(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小亮一家在东昌湖游玩,妈妈在湖心岛岸边P处观看小亮与爸爸在湖中划船(如图).小船从P处出发,沿北偏东60°划行200米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上,这时小亮与妈妈相距多少米(精确到米)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号![]() 表示不大于
表示不大于![]() 的最大整数,称
的最大整数,称![]() 为a的根整数,例如:
为a的根整数,例如:![]() ,
,![]() =3.
=3.
(1)仿照以上方法计算:![]() =______;
=______;![]() =_____.
=_____.
(2)若![]() ,写出满足题意的x的整数值______.
,写出满足题意的x的整数值______.
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次![]()
![]()
![]() =1,这时候结果为1.
=1,这时候结果为1.
(3)对100连续求根整数,____次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com