Question

13．在矩形ABCD中，AB=4，AD=6，M是AD边的中点，P是射线AB上的一个动点（不与A，B重合），MN⊥PM交射线BC于N点．
（1）如图1，当点N与点C重合时，求AP的长；
（2）如图2，在点N的运动过程中，求证：$\frac{PM}{MN}$为定值；
（3）在射线AB上，是否存在点P，使得△DCN∽△PMN？若存在，求此时AP的长；若不存在，请说明理由．

Answer 1

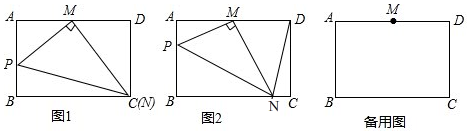
分析 （1）先判断出∠APM=∠DMC即可得出△APM∽△DMC，即$\frac{AP}{MD}$=$\frac{AM}{CD}$，再求出AM=MD=3，CD=4代入即可；
（2）分两种情况①判断出，△APM∽△DMG，和△APM∽△CNG用得出的比例式化简即可得出结论；
②同①的方法即可得出结论；
（3）先求出CN，再用△MDH∽△NCH求出DH，CH，最后用△APM∽△MDH即可求出结论．

解答 （1）∵矩形ABCD，∴∠A=∠D=90°，
∵MN⊥PM，
∴∠APM=90°-∠AMP=∠DMC，
∴△APM∽△DMC，
∴$\frac{AP}{MD}$=$\frac{AM}{CD}$，
∵点M是AD的中点，
∴MD=AM=$\frac{1}{2}$AD=3，
∵CD=AB=4，
∴$\frac{AP}{3}$=$\frac{3}{4}$，
∴AP=$\frac{9}{4}$；

（2）证明：①当点P在线段AB上时，如图2，

延长MN交DC的延长线于G，
同（1）的方法得出，△APM∽△DMG，
∴$\frac{AP}{DM}=\frac{AM}{DG}$=$\frac{PM}{MG}$，
∴$\frac{AP}{3}$=$\frac{3}{4+CG}$=$\frac{PM}{MN+NG}$，
∴$\frac{MN}{PM}$+$\frac{NG}{PM}$=$\frac{4}{3}$+$\frac{CG}{3}$，
∵AD∥CN，
∴∠CNG=∠DMG=∠APM，
∵∠PAM=∠NCG=90°，
∴△APM∽△CNG，
∴$\frac{NG}{PM}=\frac{CG}{AM}$，
∴$\frac{NG}{PM}$=$\frac{CG}{3}$，
∴$\frac{MN}{PM}$=$\frac{4}{3}$，
∴$\frac{PM}{MN}$=$\frac{3}{4}$；
②当点P在AB的延长线上时，如图，

同①的方法得出，△APM∽△DMH，
∴$\frac{PM}{MH}=\frac{AM}{DH}$，
∴$\frac{PM}{MH}=\frac{3}{CD-CH}=\frac{3}{4-CH}$，
∴$\frac{MH}{PM}=\frac{4-CH}{3}=\frac{4}{3}-\frac{CH}{3}$，
∴$\frac{MN-NH}{PM}=\frac{4}{3}-\frac{CH}{3}$，
∴$\frac{MN}{PM}-\frac{NH}{PM}=\frac{4}{3}-\frac{CH}{3}$，
同①的方法得出，△APM∽△CNH，
∴$\frac{PM}{NH}=\frac{AM}{CH}$，
∴$\frac{NH}{PM}=\frac{CH}{AM}=\frac{CH}{3}$，
∴$\frac{PM}{MN}$=$\frac{3}{4}$；
即：$\frac{PM}{MN}=\frac{3}{4}$是定值．

（3）存在点P，使得△DCN∽△PMN，
解：由（2）知$\frac{PM}{MN}$=$\frac{3}{4}$，△DCN∽△PMN时，
∴$\frac{DC}{CN}$=$\frac{PM}{MN}$，
∴$\frac{3}{CN}$=$\frac{3}{4}$，
∴CN=4，
易得，△MDH∽△NCH，
∴$\frac{MD}{CN}$=$\frac{DH}{CH}$=$\frac{3}{4}$，
∵CD=AB=4，
∴DH=$\frac{12}{7}$，CH=$\frac{16}{7}$，
由（2）②知，△APM∽△MDH，
∴$\frac{AP}{MD}$=$\frac{AM}{DH}$，
∴$\frac{AP}{3}$=$\frac{3}{\frac{12}{7}}$，
∴AP=$\frac{21}{4}$．

点评 此题是相似形综合题，主要考查了矩形的性质，同角的余角相等，相似三角形的判定和性质，中点的性质，解本题的关键是三角形相似的判定的应用，难点是准确找出相似三角形，是一道难度比较大的中考常考题．