
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点E.
求证:(1)DE⊥AE;
(2)AE+CE=AB.

【答案】证明见解析
【解析】
(1)连接OD,根据等腰三角形的性质结合角平分线的性质可得出∠CAD=∠ODA,利用“内错角相等,两直线平行”可得出AE∥OD,结合切线的性质即可证出DE⊥AE;
(2)过点D作DM⊥AB于点M,连接CD、DB,根据角平分线的性质可得出DE=DM,结合AD=AD、∠AED=∠AMD=90°即可证出△DAE≌△DAM(SAS),根据全等三角形的性质可得出AE=AM,由∠EAD=∠MAD可得出![]() ,进而可得出CD=BD,结合DE=DM可证出Rt△DEC≌Rt△DMB(HL),根据全等三角形的性质可得出CE=BM,结合AB=AM+BM即可证出AE+CE=AB.
,进而可得出CD=BD,结合DE=DM可证出Rt△DEC≌Rt△DMB(HL),根据全等三角形的性质可得出CE=BM,结合AB=AM+BM即可证出AE+CE=AB.
(1)连接OD,如图1所示.
∵OA=OD,AD平分∠BAC,
∴∠OAD=∠ODA,∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴AE∥OD.
∵DE是⊙O的切线,
∴∠ODE=90°,
∴OD⊥DE,
∴DE⊥AE.
(2)过点D作DM⊥AB于点M,连接CD、DB,如图2所示.
∵AD平分∠BAC,DE⊥AE,DM⊥AB,
∴DE=DM.
在△DAE和△DAM中,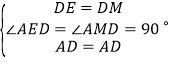 ,
,
∴△DAE≌△DAM(SAS),
∴AE=AM.
∵∠EAD=∠MAD,
∴![]() ,
,
∴CD=BD.
在Rt△DEC和Rt△DMB中,![]() ,
,
∴Rt△DEC≌Rt△DMB(HL),
∴CE=BM,
∴AE+CE=AM+BM=AB.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:![]() ≈1.73,
≈1.73,![]() ≈1.41).
≈1.41).
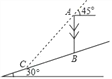
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明命题“对角线相等的平行四边形是矩形”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小张同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,ABCD是平行四边形,AC与BD是对角线,且 .
求证: .
请你补全已知和求证,并写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学之道在于悟,希望同学们在问题(1)解决过程中有所感悟,再继续探索研究问题(2)(3).
(1)如图①,D在线段BC上,∠B=∠C=∠ADE,AD=DE.求证:△ABD≌△DCE.
(2)如图②,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=4,在CB的延长线上有一动点D,连接AD,以AD为直角边作等腰直角三角形ADE(∠ADE=90°,AD=DE ),连接EB并延长,与AC的延长线交于点F.当动点D在运动过程中,CF的长度是否会发生变化,如果变化,请说明理由;如果不变,请求出CF的长.
(3)如图③,射线AM与BN,MA⊥AB,NB⊥AB,点P是AB上一点, PA=1,PB=2,在射线AM与BN上分别作点C、点D,满足△CPD为等腰直角三角形.则△CPD的面积为 .
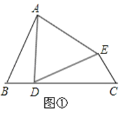


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船从A港出发,以28海里/小时的速度向正北方向航行,此时测的灯塔M在北偏东30°的方向上.半小时后,轮船到达B处,此时测得灯塔M在北偏东60°的方向上.
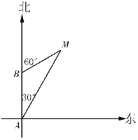
(1)求轮船在B处时与灯塔M的距离;
(2)轮船从B处继续沿正北方向航行,又经半小时后到达C处.求:此时轮船与灯塔M的距离是多少?灯塔M在轮船的什么方向上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 经过某种变换后得到点
经过某种变换后得到点![]() ,我们把点
,我们把点![]()
![]() 叫做点
叫做点![]() 的终结点.已知点
的终结点.已知点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,这样依次得到
,这样依次得到![]() 、
、![]() 、
、![]() 、
、![]() …
…![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BC=2![]() .点P从点A出发沿沿射线AB以1
.点P从点A出发沿沿射线AB以1![]() 的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1
的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1![]() 的速度运动,连结BE、EQ.设点P的运动时间为t(
的速度运动,连结BE、EQ.设点P的运动时间为t(![]() ).
).

(1)求证:△APE是等边三角形;
(2)直接写出CE的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点P在边AB上,且不与点A、B重合时,求证:△BPE≌△ECQ.
(4)在不添加字母和连结其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com