
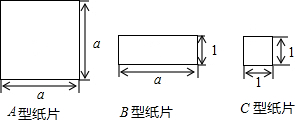
分析 (1)由于1块A型的面积为a2cm,1快、块B型的面积为4acm2,1块C型的面积为4cm2,所以A型2块,B型4块,C型4块的总面积为(2a2+4a+4)cm2;
①把2a2+4a+4减去a2,然后根据完全平方公式得到a2+4a+4=(a+2)2,由此得到正方形的边长;
②把2a2+4a+4减去2,然后根据完全平方公式得到2a2+4a+2=2(a+1)2,由此得到正方形的边长与面积,所以从这10块纸板中拿掉2块C类型的纸板满足要求;
(2)从这28块纸板中拿掉1块C类型的纸板可满足要求,因为12a2+12a+4-1=12a2+12a+3=3(2a+1)2,此时正方形的边长为(2a+1)cm.
解答 解:(1)1块A型的面积为a2cm,1快、块B型的面积为4acm2,1块C型的面积为4cm2,
所以A型2块,B型4块,C型4块的总面积为(2a2+4a+4)cm2;
①这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形.
剩下纸板的总面积为2a2+4a+4-a2=a2+4a+4,而a2+4a+4=(a+2)2,
则此正方形的边长为(a+2)cm;
②从这10块纸板中拿掉2块C类型的纸板,使得剩下的纸板在不重叠的情况下,
可以紧密地排出两个相同的大正方形.
理由如下:
2a2+4a+4-2=2a2+4a+2=2(a2+2a+1)=2(a+1)2,
此时正方形的边长为(a+1)cm,
则正方形面积为:(a+1)2=(a2+2a+1);
(2)∵12a2+12a+4-1=12a2+12a+3=3(2a+1)2,
∴此时正方形的边长为(2a+1)cm.
故答案为:(2a2+4a+4),a+2;(2a+1)cm.
点评 本题考查了完全平方公式的几何背景:运用几何直观理解、解决完全平方公式的推导过程,通过几何图形之间的数量关系对完全平方公式做出几何解释.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:| R | … | 2 | 4 | 8 | 10 | 16 | … |
| I | … | 16 | 8 | 4 | 3.2 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
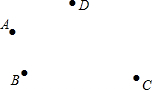 平面上有四个点A、B、C、D,按照以下要求作图:
平面上有四个点A、B、C、D,按照以下要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
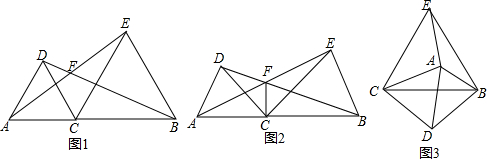
 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
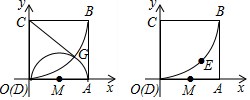 如图,正方形ABCD的顶点A,C分别在x轴,y轴正半轴上,点B的坐标为(10,10),以点C为圆心,CB为半径画弧OB.
如图,正方形ABCD的顶点A,C分别在x轴,y轴正半轴上,点B的坐标为(10,10),以点C为圆心,CB为半径画弧OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com