
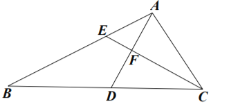
【题目】如图,在![]() 中,
中,![]() 为三角形的角平分线,
为三角形的角平分线,![]() 于点
于点![]() 交
交![]() 于点
于点![]()
(1)若![]() ,直接写出
,直接写出![]() 度
度
(2)若![]() ,
,
①求证:![]()
②若![]() ,直接写出
,直接写出![]() (用含
(用含![]() 的式子表示)
的式子表示)
【答案】(1)![]() ;(2)①见详解;②
;(2)①见详解;②![]()
【解析】
(1)由三角形内角和定理和角平分线定义即可得出答案;
(2)①证明![]() ,得出BE=CE,过点A作
,得出BE=CE,过点A作![]() 交CE与点H,则
交CE与点H,则![]() ,得出AH=AC,
,得出AH=AC,![]() ,得出AE=HE,由等腰三角形的性质可得出HF=CF,即可得出结论;
,得出AE=HE,由等腰三角形的性质可得出HF=CF,即可得出结论;
②证明![]() ,得出AH=DC,求出HF=CF=a,HE=HF-EF=a-b,CE=a+b,由
,得出AH=DC,求出HF=CF=a,HE=HF-EF=a-b,CE=a+b,由![]() 得出
得出![]() ,进而得出结论.
,进而得出结论.
解:(1)∵![]() ,
,
∴![]() ,
,
∵![]() 为三角形的角平分线,
为三角形的角平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为:![]() ;
;
(2)①证明:∵![]()
∴![]()
∴![]()
过点A作![]() 交CE与点H,如图所示:
交CE与点H,如图所示:
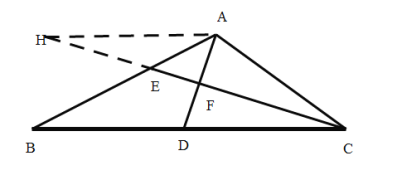
则![]()
∴AH=AC,![]()
∴AE=HE
∵![]()
∴HF=CF
∴AB=HC=2CF;
②在![]() 和
和![]() 中,
中,
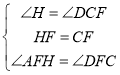
∴![]()
∴AH=DC
∵![]()
∴![]() ,由①得
,由①得![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]() .
.
故答案为:![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,若添加一个条件不能得到“△ABD≌△ACE”是( )
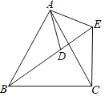
A. ∠ABD=∠ACE B. BD=CE C. ∠BAD=∠CAE D. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:

①A、B之间的距离为1200m; ②乙行走的速度是甲的1.5倍;③ b=960; ④ a=34.
以上结论正确的有( )
A. ①② B. ①②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点
边的中点
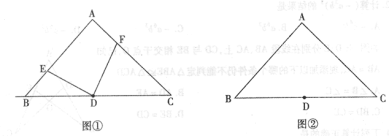
(1)如图①,点![]() 分别为边
分别为边![]() 上的点
上的点![]() ,且
,且![]() .若,则
.若,则![]()
![]() ;若
;若![]() ,则四边形
,则四边形![]() 的面积为
的面积为
(2)若点![]() 分别为
分别为![]() 延长线上的点,且
延长线上的点,且![]() ,那么
,那么![]() 吗?请利用图②说明理由.
吗?请利用图②说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com