
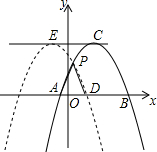
 如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.
如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.分析 (1)不存在,不妨设△PAD是直角三角形,过点P作PQ⊥AD于Q,可以推出AD=2PQ,列出方程,推出矛盾即可解决问题.
(2)首先判断只存在△CAF∽△PAD这种情形,如图2中,过点C作CM⊥x轴于点M,点A作AN⊥CF于点N,过点A作AG⊥PD于点G,先求出点F坐标,设PG=3x,则AG=4x,列出方程即可解决问题.
解答 解:(1)令y=0,则-$\frac{4}{9}$(x-2)2+4=0,
解得x=-1或5,
∴A(-1,0),B(5,0),C(2,4),
如图1中,过点P作PQ⊥AD于Q,根据对称性可知PA=PD,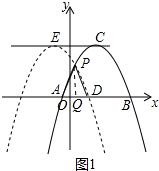
∴△PAD是等腰三角形,
设D(5-m,0),则Q($\frac{4-m}{2}$,0),
∴P($\frac{4-m}{2}$,-$\frac{1}{9}$m2+4),
若△PAD是直角三角形,则△PAD是等腰直角三角形,∠APD=90°,
∴AD=2PQ,
∴(5-m)+1=2(-$\frac{1}{9}$m2+4),
整理得2m2-9m-18=0,
解得m=6或m=-$\frac{3}{2}$,
∵m>0,
∴m=6,
当m=6时,P(-1,0)与点A重合,故舍弃.
∴△PAD不能成为直角三角形.
(2)由(1)可知,△PAD是等腰三角形,连接AC,则∠CAD<∠PAD=∠PDA,
∵CE∥AD,
∴∠FCA=∠CAD<∠PAD=∠PDA,
∴以A、C、F为顶点的三角形与△PAD相似,只存在△CAF∽△PAD这种情形,
∴$\frac{CA}{CF}$=$\frac{PA}{PD}$=1,
∴CA=CF,
如图2中,过点C作CM⊥x轴于点M,则点M(2,0),
∴AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=5,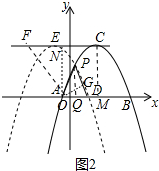
∴CF=5,
∴F(-3,4),
过点A作AN⊥CF于点N,则点N(-1,0).
过点A作AG⊥PD于点G,则∠APG=∠ACN,
∴tan∠APG=tan∠ACN=$\frac{CN}{AN}$=$\frac{4}{3}$,
设PG=3x,则AG=4x,
∴AP=$\sqrt{A{G}^{2}+P{G}^{2}}$=5x,
∴DG=5x-3x=2x,
∴AD=$\sqrt{D{G}^{2}+A{G}^{2}}$=2$\sqrt{5}$x,
∵$\frac{1}{2}$•AD•PQ=$\frac{1}{2}$•PD•AG,
∴PQ=2$\sqrt{5}$x=AD,
∴-$\frac{1}{9}$m2+4=5-m+1,
整理得m2-9m+18=0,
解得m=3或m=6.
当m=6时,P(-1,0)与点A重合,故舍弃,
∴m=3.
点评 本题考查二次函数综合题、平移、相似三角形的判定和性质、直角三角形、勾股定理等知识,解题的关键是学会用方程的思想思考问题,利用相似三角形性质、面积法、勾股定理构建方程解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 小东从甲地出发匀速前往相距20km的乙地,一段时间后,小明从乙地出发沿同一条路匀速前往甲地.小东出发2.5h后,在距乙地7.5km处与小明相遇,之后两人同时到达终点.图中线段AB、CD分别表示小东、小明与乙地的距离y(km)与小东所用时间x(h)的关系.
小东从甲地出发匀速前往相距20km的乙地,一段时间后,小明从乙地出发沿同一条路匀速前往甲地.小东出发2.5h后,在距乙地7.5km处与小明相遇,之后两人同时到达终点.图中线段AB、CD分别表示小东、小明与乙地的距离y(km)与小东所用时间x(h)的关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
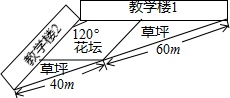 学校两幢教学楼之间有一块三角形地带,将其划分为三个区域:一块菱形和两块三角形.菱形作为花坛,两个三角形内铺上草皮,两幢教学楼的夹角为120°,其余尺寸如图所示,则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2.
学校两幢教学楼之间有一块三角形地带,将其划分为三个区域:一块菱形和两块三角形.菱形作为花坛,两个三角形内铺上草皮,两幢教学楼的夹角为120°,其余尺寸如图所示,则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
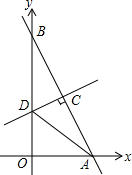 如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x-4)+8(4-x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.
如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x-4)+8(4-x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com