
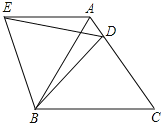
【题目】在边长为3的正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA边上,且满足EB=FC=GD=HA=1,BD分别与HG、HF、EF相交于M、O、N给出以下结论:
①HO=OF;②OF2=ONOB;③HM=2MG;④S△HOM=![]() ,其中正确的个数有( )
,其中正确的个数有( )
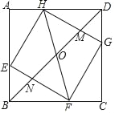
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
根据正方形的性质、全等三角形的判定和性质、角平分线的性质定理一一判断即可.
作MP⊥AD于P,MQ⊥CD于Q.连接OG.
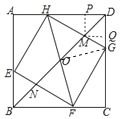
∵四边形ABCD是正方形,∴AD∥BC,AD=BC.
∵AH=CF,∴DH=BF,∠ODH=∠OBF.
∵∠DOH=∠BOF,∴△DOH≌△BOF,∴OH=OF,故①正确.
∵∠FON=∠FOB,∠OFN=∠OBF=45°,∴△OFN∽△OBF,∴OF2=ONOB,故②正确.
∵∠MDH=∠MDG,MP⊥AD于P,MQ⊥CD于Q,∴MP=MQ.
∵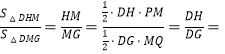 2,∴HM=2MG,故③正确.
2,∴HM=2MG,故③正确.
∵正方形EFGH的面积=5,∴S△OHG的面积![]() ,∴S△OMH
,∴S△OMH![]() ,故④正确.
,故④正确.
故选D.


科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
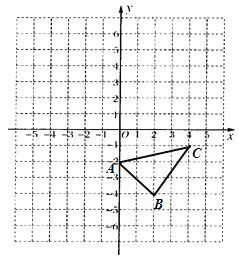
【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标:
三个顶点的坐标: ![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)直接写出△ABC的面积为 ;
(3)在![]() 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() 是边
是边![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则有以下四个结论:①
,则有以下四个结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() 的周长是10;④
的周长是10;④![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
A.②③④B.①③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
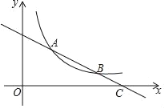
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象相交于A(2,3)、B(a,1)两点.
(x>0)的图象相交于A(2,3)、B(a,1)两点.
(1)求这两个函数的表达式;
(2)求证:AB=2BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图(1)、(2)所示的△ABC中,AB=4,AC=6.将△ABC沿图示中的虚线剪开裁剪办法已在图上标注,对于各图中剪下的两个阴影三角形而言,下列说法正确的是( )
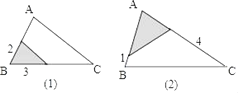
A. 只有(1)中的与△ABC相似 B. 只有(2)中的与△ABC相似
C. 都与△ABC相似 D. 都与△ABC不相似
查看答案和解析>>
科目:初中数学 来源: 题型:
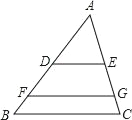
【题目】如图,在△ABC中,点D,F在AB上,点E,G在AC上,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形FBCG
(1)求DE:FG:BC的值;
(2)若AB=10,AC=15,BC=12,求四边形DFGE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com