
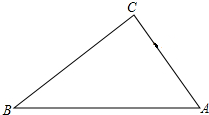
 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→B→A直线运动,且速度为每秒2cm,设出发的时间为t秒.
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→B→A直线运动,且速度为每秒2cm,设出发的时间为t秒.分析 (1)由勾股定理求出AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4cm,由题意得出PC=1cm,则BP=BC-PC=2cm,由勾股定理求出AP,即可得出△ABP的周长;
(2)分三种情况:①当PC=PB时,点P在BC的垂直平分线上,则P为AB的中点,得出2t=3+2.5,解方程即可;
②当BP=BC=3cm时,2t=3+3,解方程即可;
③当CP=CB时,作CD⊥AB于D,由三角形的面积关系求出CD,由勾股定理求出BD,得出BP,由题意得出2t=3+$\frac{18}{5}$,解方程即可;
(3)分两种情况,由题意得出方程,解方程即可.
解答 解:(1)∵∠C=90°,AB=5cm,BC=3cm,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4cm,
当t=$\frac{1}{2}$s时,PC=1cm,
∴BP=BC-PC=2cm,AP=$\sqrt{A{C}^{2}+P{C}^{2}}$=$\sqrt{{4}^{2}+{1}^{1}}$=$\sqrt{17}$(cm),
∴△ABP的周长=AB+PA+BP=5+$\sqrt{17}$+2=7+$\sqrt{17}$(cm);
(2)分三种情况: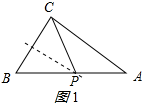
①当PC=PB时,点P在BC的垂直平分线上,
则P为AB的中点,如图1所示:
∴BP=2.5,
∴2t=3+2.5,
解得:t=$\frac{11}{4}$;
②当BP=BC=3cm时,如图2所示: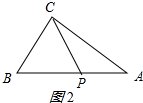
2t=3+3,
解得:t=3;
③当CP=CB时,作CD⊥AB于D,
如图3所示:
则CD=$\frac{AC•BC}{AB}$=$\frac{4×3}{5}$=$\frac{12}{5}$(cm),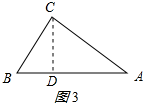 ∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=$\frac{9}{5}$cm,
∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=$\frac{9}{5}$cm,
∴BP=2BD=$\frac{18}{5}$cm,
∵2t=3+$\frac{18}{5}$,
∴t=$\frac{33}{10}$;
综上所述:t=$\frac{11}{4}$s,或t=3s,或t=$\frac{33}{10}$s时,△BCP为等腰三角形;
(3)由题意得:
P、Q相遇前:t+2t=$\frac{3+4+5}{2}$,
解得:t=2,
P、Q相遇后:t+2t-(3+4+5)=$\frac{3+4+5}{2}$,
解得:t=6,
,即t=2s或6s时,线PQ把△ABC的周长分成相等的两部分.
点评 本题考查了勾股定理、等腰三角形的判定、三角形面积的计算方法等知识;本题有一定难度,特别是(2)中,需要进行分类讨论才能得出结果.


科目:初中数学 来源: 题型:选择题
| A. | 十分位 | B. | 百分位 | C. | 千位 | D. | 百位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
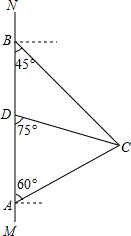 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
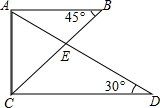 将一副三角尺如图所示叠放在一起,则$\frac{{{S_{△ABE}}}}{{{S_{△ACE}}}}$=$\frac{\sqrt{3}}{3}$.
将一副三角尺如图所示叠放在一起,则$\frac{{{S_{△ABE}}}}{{{S_{△ACE}}}}$=$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
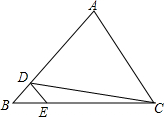 如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )
如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )| A. | 64 | B. | 72 | C. | 80 | D. | 96 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com