
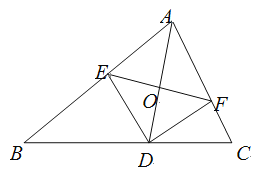
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④![]() .上述结论中正确的是( )
.上述结论中正确的是( )
A. ②③ B. ②④ C. ①②③ D. ②③④
【答案】D
【解析】只要证明△ADE≌△ADF,推出AE=EF,DE=DF,推出AD垂直平分线段EF,即可判定②③正确,利用勾股定理即可判定④正确,①不一定成立故错误.
解:∵AD是△ABC的角平分线,
∴∠DAE=∠DAF,
又∵∠AED=∠AFD=90°,AD=AD,
∴△ADE≌△ADF,
∴AE=AF,DE=DF,
∴AD垂直平分EF,故②正确,
∵∠AED=∠AFD=90°,
∴当∠EAF=90°时,
∴四边形AEDF是矩形,
∵AE=AF,
∴四边形AEDF是正方形,故③正确,
∵AE2+DF2=EO2+AO2+OD2+OF2,
DE2+AF2=OE2+OD2+OA2+OF2,
∴AE2+DF2=AF2+DE2,故④正确,
∵AD垂直平分EF,
而EF不一定垂直平分AD,故①错误,
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
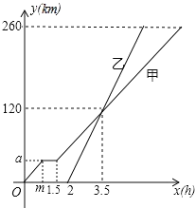
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)直接写出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x (h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车出发多长时间后,两车恰好相距40km?
查看答案和解析>>
科目:初中数学 来源: 题型:
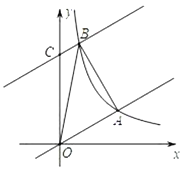
【题目】如图,在平面直角坐标系中,直线![]() ,与反比例函数
,与反比例函数![]() 在第一象限内的图象相交于点
在第一象限内的图象相交于点![]()
(1)求该反比例函数的表达式;
(2)将直线![]() 沿
沿![]() 轴向上平移
轴向上平移![]() 个单位后与反比例函数在第一象限内的图象相交于点
个单位后与反比例函数在第一象限内的图象相交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,连接
,连接![]() ,
,![]() .
.
①求![]() 的值;
的值;
②判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)在(2)的条件下,在射线![]() 上有一点
上有一点![]() (不与
(不与![]() 重合),使
重合),使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学实践活动中,观测小组对某品牌节能饮水机进行了观察和记录,当观察到第![]() 分钟时,水温为
分钟时,水温为![]() ,记录的相关数据如下表所示:
,记录的相关数据如下表所示:
第一次加热、降温过程 | … | |||||||||||
t(分钟) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | … |
y( | 20 | 40 | 60 | 80 | 100 | 80 | 66.7 | 57.1 | 50 | 44.4 | 40 | … |
(饮水机功能说明:水温加热到![]() 时饮水机停止加热,水温开始下降,当降到
时饮水机停止加热,水温开始下降,当降到![]() 时饮水机又自动开始加热)
时饮水机又自动开始加热)
请根据上述信息解决下列问题:
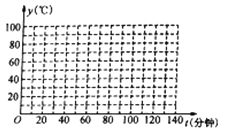
(1)根据表中数据在如给出的坐标系中,描出相应的点;
(2)选择适当的函数,分别求出第一次加热过程和第一次降温过程![]() 关于
关于![]() 的函数关系式,并写出相应自变量的取值范围;
的函数关系式,并写出相应自变量的取值范围;
(3)已知沏茶的最佳水温是![]() ,若18:00开启饮水机(初始水温
,若18:00开启饮水机(初始水温![]() )到当晚20:10,沏茶的最佳水温时间共有多少分钟?
)到当晚20:10,沏茶的最佳水温时间共有多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
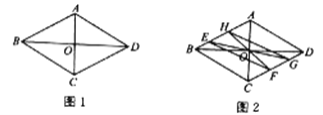
【题目】如图1,点![]() 是菱形
是菱形![]() 对角线的交点,已知菱形的边长为12,
对角线的交点,已知菱形的边长为12,![]() .
.
(1)求![]() 的长;
的长;
(2)如图2,点![]() 是菱形边上的动点,连结
是菱形边上的动点,连结![]() 并延长交对边于点
并延长交对边于点![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交菱形于点
交菱形于点![]() ,延长
,延长![]() 交对边于点
交对边于点![]() .
.
①求证:四边形![]() 是平行四边形;
是平行四边形;
②若动点![]() 从点
从点![]() 出发,以每秒1个单位长度沿
出发,以每秒1个单位长度沿![]() 的方向在
的方向在![]() 和
和![]() 上运动,设点
上运动,设点![]() 运动的时间为
运动的时间为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 为矩形.
为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
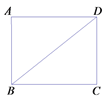
【题目】如图,在矩形ABCD中,对角线BD的长为1,点P是线段BD上的一点,联结CP,将△BCP沿着直线CP翻折,若点B落在边AD上的点E处,且EP//AB,则AB的长等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
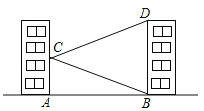
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形桌子可坐6人,按图3将桌子拼在一起.

(1)2张桌子拼在一起可坐 人,4张桌子拼在一起可坐 人,n张桌子拼在一起可坐 人;
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com