
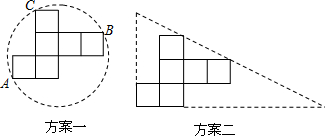
 ×100%
×100%
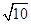 ,AB=
,AB=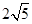

 =
= ,
, =
= ,
, ×100%=
×100%= ×100%=37.5%;
×100%=37.5%;
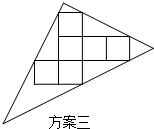
 a,
a,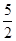 a,
a,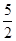 a=
a= a,GL=
a,GL= a,
a,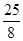 a,
a,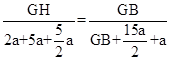 ,
,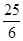 a,
a, a,AC=
a,AC= a,
a, ×AB×AC=
×AB×AC= a2,
a2, ×100%=
×100%=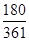 ×100%=49.86%.
×100%=49.86%. ,AB=
,AB=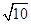 ,根据勾股定理的逆定理,即可求得∠BAC=90°,又由90°的圆周角所对的弦是直径,则可证得AB为该圆的直径;
,根据勾股定理的逆定理,即可求得∠BAC=90°,又由90°的圆周角所对的弦是直径,则可证得AB为该圆的直径;

 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
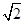 BM;
BM; ,且AF:FD=1:2时,求线段DG的长.
,且AF:FD=1:2时,求线段DG的长.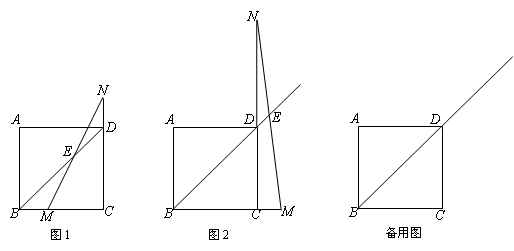
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题


| A.(6,0) | B.(6,3) |
| C.(6,5) | D.(4,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com