

 DG=
DG= GF,在直角三角形FGH中,利用勾股定理可得HF=
GF,在直角三角形FGH中,利用勾股定理可得HF=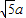 ,从而用含a的代数式表示半圆的半径为
,从而用含a的代数式表示半圆的半径为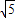 a,正方形边长为2a,所以可求得半圆的半径与正方形边长的比;
a,正方形边长为2a,所以可求得半圆的半径与正方形边长的比;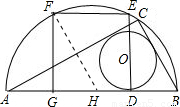 解:①如图,根据圆和正方形的对称性可知:GH=
解:①如图,根据圆和正方形的对称性可知:GH= DG=
DG= GF,
GF,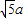 .由此可得,半圆的半径为
.由此可得,半圆的半径为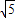 a,正方形边长为2a,
a,正方形边长为2a,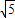 a:2a=
a:2a=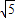 :2;
:2;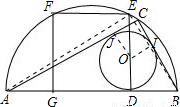


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源:2011年浙江省杭州市余杭区良渚中学中考数学模拟试卷(吴建德)(解析版) 题型:解答题
 a(要求保留作图痕迹,不必写出作法);
a(要求保留作图痕迹,不必写出作法);
查看答案和解析>>
科目:初中数学 来源:2011年中考复习专项训练《线段、角、相交线、平行线》(解析版) 题型:解答题
 (2009•杭州)如图,在等腰梯形ABCD中,∠BCD=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE于点P.
(2009•杭州)如图,在等腰梯形ABCD中,∠BCD=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE于点P.查看答案和解析>>
科目:初中数学 来源:2011年中考复习专项训练《三角形的边和角》(解析版) 题型:解答题
 a(要求保留作图痕迹,不必写出作法);
a(要求保留作图痕迹,不必写出作法);
查看答案和解析>>
科目:初中数学 来源:2009年浙江省杭州市中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com