Question

7．如图，二次函数y=-x²+$\frac{5}{3}$x+4与x轴交于A、B两点，与y轴交于点C，点P从点O出发沿OA以每秒1个单位长度的速度向点A运动，到达点A后立刻在以原来的速度沿AO返回；点Q从点A出发沿AC以每秒1个单位长度的速度向点C匀速运动，过点Q作QD⊥x轴，垂足为D．点P、Q同时出发，当点Q到达点C时停止运动，点P也随之停止．设点P，Q的运动时间为t（t≥0）．

（1）当点P从点O向点A运动的过程中，求△QPA面积S与t的函数关系式；
（2）当线段PQ与抛物线的对称轴没有公共点时，请直接写出t的取值范围；
（3）当t为何值时，以P、D、Q为顶点的三角形与△OBC相似；
（4）如图2：FE保持垂直平分PQ，且交PQ于点F，交折线QC-CO-OP于点E，在整个运动过程中，请你直接写出点E所经过的路径长．

Answer 1

分析 （1）如图1，根据已知得：点P从点O向点A运动的时间为0≤t≤3，作△QPA的高QE，分别表示出AP和QE的长，利用面积公式代入计算即可；
（2）作出对称轴，当线段PQ与抛物线的对称轴没有公共点时，P应该在对称轴的右侧，所以要先计算对称轴，即t＞$\frac{5}{6}$，点Q也应该在对称轴的右侧，所以要计算AF的长，满足AQ＜AF，从而得出结论；
（3）分四种情况讨论：①当△BOC∽△QDP时，如图3，根据对应边成比例列方程解出即可；②如图4，当△BOC∽△PDQ时；③如图5，当△BOC∽△PDQ时；④如图6，当△BOC∽△PDQ时；同理依次算出t的值，注意在四种情况下，PD的值不同，要分别根据图形计算；
（4）点E所经过的路径从t=0时开始：点E开始在AC的中点处，当0≤t≤3时，E～C～O～E，当3＜t≤5时，点P从点A向左运动，点E的运动路径是：图8的点E～O～图9中的点E，分别计算各条线段的长，并相加即可．

解答 解：（1）如图1，y=-x²+$\frac{5}{3}$x+4，
y=0时，-x²+$\frac{5}{3}$x+4=0，
解得：x₁=3，x₂=-$\frac{4}{3}$，
∴A（3，0），B（-$\frac{4}{3}$，0），
x=0时，y=4，则OC=4，AC=5，
∵OA=3，
∴0≤t≤3，
由题意得：OP=t，AQ=t，
过Q作QE⊥x轴于E
∴QE∥y轴，
∴$\frac{AQ}{AC}=\frac{QE}{OC}$，
∴$\frac{t}{5}=\frac{QE}{4}$，
∴QE=$\frac{4t}{5}$，
∴S=S_△APQ=$\frac{1}{2}$AP•QE=$\frac{1}{2}$×（3-t）•$\frac{4t}{5}$=-$\frac{2{t}^{2}}{5}$+$\frac{6t}{5}$；
（2）对称轴：x=-$\frac{\frac{5}{3}}{2×（-1）}$=$\frac{5}{6}$，
∴t＞$\frac{5}{6}$，
∵FG∥y轴，
∴$\frac{AF}{AC}=\frac{AG}{AO}$，
∴$\frac{AF}{5}=\frac{3-\frac{5}{6}}{3}$，
∴AF=$\frac{65}{18}$，
∴t＜$\frac{65}{18}$，
∴当$\frac{5}{6}$＜t＜$\frac{65}{18}$时，线段PQ与抛物线的对称轴没有公共点；
（3）OP=t，AP=3-t，AQ=t，DQ=$\frac{4t}{5}$
①当△BOC∽△QDP时，如图3，
∵QD∥y轴，
∴$\frac{AQ}{AC}=\frac{AD}{OA}$，
∴$\frac{t}{5}=\frac{AD}{3}$，
∴AD=$\frac{3t}{5}$，
∴PD=3-t-$\frac{3t}{5}$=-$\frac{8t}{5}$+3，
∵$\frac{OB}{QD}=\frac{OC}{DP}$，
∴$\frac{\frac{4}{3}}{\frac{4t}{5}}$=$\frac{4}{-\frac{8t}{5}+3}$，
∴t=$\frac{3}{4}$；
②如图4，当△BOC∽△PDQ时，
∴$\frac{OB}{PD}=\frac{OC}{DQ}$，
∴$\frac{\frac{4}{3}}{-\frac{8t}{5}+3}$=$\frac{4}{\frac{4t}{5}}$，
∴t=$\frac{45}{28}$；
③如图5，当△BOC∽△PDQ时，PD=OP+AD-OA=t+$\frac{3t}{5}$-3=$\frac{8t}{5}$-3，
∴$\frac{OB}{PD}=\frac{OC}{DQ}$，
∴$\frac{\frac{4}{3}}{\frac{8t}{5}-3}$=$\frac{4}{\frac{4t}{5}}$，
∴t=$\frac{9}{4}$；
④如图6，当△BOC∽△PDQ时，PD=AD-AP=$\frac{3t}{5}$-（t-3）=-$\frac{2t}{5}$+3，
∵QD∥y轴，
∴$\frac{OB}{PD}=\frac{OC}{DQ}$，
∴$\frac{\frac{4}{3}}{-\frac{2t}{5}+3}$=$\frac{4}{\frac{4t}{5}}$，
∴t=$\frac{9}{2}$；
综上所述：当t=$\frac{3}{4}$或$\frac{45}{28}$或$\frac{9}{4}$或$\frac{9}{2}$时，以P、D、Q为顶点的三角形与△OBC相似；
（4）当t=0时，如图7，P在O点，Q在A点，
∵EF是OA的垂直平分线，
∴E是AC的中点，
∴EC=$\frac{5}{2}$，
当t=3时，P在A点，Q在AC上，则AQ=3，AF=$\frac{3}{2}$，
cos∠A=$\frac{AF}{AE}=\frac{OA}{AC}$，
∴$\frac{\frac{3}{2}}{AE}$=$\frac{3}{5}$，
∴AE=$\frac{5}{2}$，
∴OE=3-$\frac{5}{2}$=$\frac{1}{2}$，
当t=5时，Q在C点，P在OA上，连接EP，则CE=EP，
设EP=x，则OE=4-x，
则x²=（4-x）²+1²，
解得：x=$\frac{17}{8}$，
∴OE=4-$\frac{17}{8}$=$\frac{15}{8}$；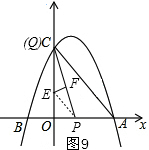
∴点E所经过的路径长=$\frac{5}{2}$+4+$\frac{1}{2}$+$\frac{1}{2}$+$\frac{15}{8}$=$\frac{75}{8}$；
则点E所经过的路径长为$\frac{75}{8}$．

点评 本题是二次函数的综合题，综合性较强，是运动型问题；此类题的关键是要弄清动点的运动路径，一般从动点运动过程中的某些特殊位置入手，从开始到停止，认真观察各时间所形成的图形；对于两直角三角形相似，如果不确定对应边时，要分情况进行讨论．