
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.

A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】
取AD的中点F,连接EF.根据平行线的性质可证得(1)(4)(5),根据梯形中位线定理可证得(3)正确.根据全等三角形全等的判定可证得(2)的正误,即可得解.
解:如图:取AD的中点F,连接EF.
∵∠B=∠C=90°,
∴AB∥CD;[结论(5)]
∵E是BC的中点,F是AD的中点,
∴EF∥AB∥CD,2EF=AB+CD(梯形中位线定理)①;
∴∠CDE=∠DEF(两直线平等,内错角相等),
∵DE平分∠ADC,
∴∠CDE=∠FDE=∠DEF,
∴DF=EF;
∵F是AD的中点,∴DF=AF,
∴AF=DF=EF②,
由①得AF+DF=AB+CD,即AD=AB+CD;[结论(3)]
由②得∠FAE=∠FEA,
由AB∥EF可得∠EAB=∠FEA,
∴∠FAE=∠EAB,即EA平分∠DAB;[结论(1)]
由结论(1)和DE平分∠ADC,且DC∥AB,可得∠EDA+∠DAE=90°,则∠DEA=90°,即AE⊥DE;[结论(4)].
由以上结论及三角形全等的判定方法,无法证明△EBA≌△DCE.
正确的结论有4个.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=![]() ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有以下三角形:①三角形三边之比为2:3:2;②三角形的三边为3,4,5;③三角形三个角分别为20°,70°,90°;④三角形三个角的比为1:2:3.其中不是直角三角形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.H是BC边上的中点,连接DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF;
BF;
(3)请你根据该题的条件并结合图形,自己提出一个问题,并解答或证明你提出的问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.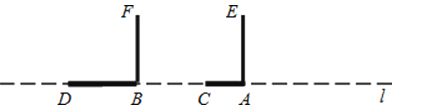
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧AB上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则△PDE的周长是( )
A.4
B.8
C.12
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com