
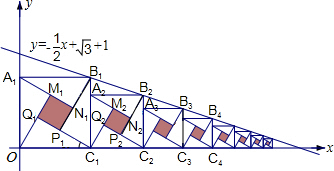
 2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线y=-
2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线y=-| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
 2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽弦图为基础设计的,弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cosθ的值等于
2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽弦图为基础设计的,弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cosθ的值等于查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省温州市四九年级下学期一模数学试卷(解析版) 题型:选择题
如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )
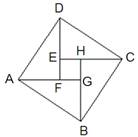
A.1:5 B.1:25 C.5:1 D.25:1
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖北恩施州卷)数学解析版 题型:填空题
(2011•恩施州)2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线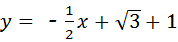 和x轴上,则第n个阴影正方形的面积为
和x轴上,则第n个阴影正方形的面积为 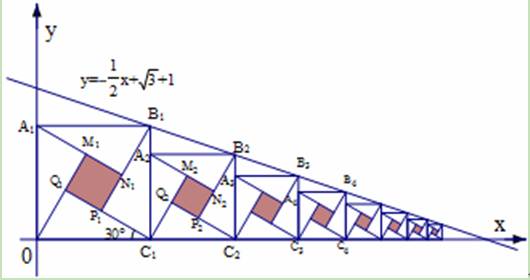
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com