
分析 (1)首先把根式$\sqrt{{x}^{2}+42}+\sqrt{{x}^{2}+10}$有理化,然后分别求出根式$\sqrt{{x}^{2}+42}+\sqrt{{x}^{2}+10}$和它的有理化因式的值是多少;再根据求出的根式$\sqrt{{x}^{2}+42}+\sqrt{{x}^{2}+10}$和它的有理化因式的值,求出方程$\sqrt{{x^2}+42}+\sqrt{{x^2}+10}=16$的解是多少即可;
(2)首先把根式$\sqrt{4{x}^{2}+6x-5}$+$\sqrt{4{x}^{2}-2x-5}$有理化,然后分别求出根式$\sqrt{4{x}^{2}+6x-5}$+$\sqrt{4{x}^{2}-2x-5}$和它的有理化因式的值是多少;再根据求出的根式$\sqrt{4{x}^{2}+6x-5}$+$\sqrt{4{x}^{2}-2x-5}$和它的有理化因式的值,求出方程$\sqrt{4{x}^{2}+6x-5}$+$\sqrt{4{x}^{2}-2x-5}$=4x的解是多少即可.
解答 解:(1)($\sqrt{{x}^{2}+42}+\sqrt{{x}^{2}+10}$)($\sqrt{{x}^{2}+42}$-$\sqrt{{x}^{2}+10}$)
=${(\sqrt{{x}^{2}+42})}^{2}$-${(\sqrt{{x}^{2}+10})}^{2}$
=(x2+42)-(x2+10)
=32
∵$\sqrt{{x^2}+42}+\sqrt{{x^2}+10}=16$,
∴$\sqrt{{x}^{2}+42}$-$\sqrt{{x}^{2}+10}$=32÷16=2,
∴$\left\{\begin{array}{l}{\sqrt{{x}^{2}+42}=9}\\{\sqrt{{x}^{2}+10}=7}\end{array}\right.$
∵${(\sqrt{{x}^{2}+42})}^{2}{=x}^{2}+42$=92=81,
∴x=±$\sqrt{39}$,
经检验x=±$\sqrt{39}$都是原方程的解,
∴方程$\sqrt{{x^2}+42}+\sqrt{{x^2}+10}=16$的解是:x=±$\sqrt{39}$;
(2)($\sqrt{4{x}^{2}+6x-5}$+$\sqrt{4{x}^{2}-2x-5}$)($\sqrt{4{x}^{2}+6x-5}$-$\sqrt{4{x}^{2}-2x-5}$)
=${(\sqrt{{4x}^{2}+6x-5})}^{2}$${-(\sqrt{{4x}^{2}-2x-5})}^{2}$
=(4x2+6x-5)-(4x2-2x-5)
=8x
∵$\sqrt{4{x}^{2}+6x-5}$+$\sqrt{4{x}^{2}-2x-5}$=4x,
∴$\sqrt{4{x}^{2}+6x-5}$-$\sqrt{4{x}^{2}-2x-5}$=8x÷4x=2,
∴$\left\{\begin{array}{l}{\sqrt{{4x}^{2}+6x-5}=2x+1}\\{\sqrt{{4x}^{2}-2x-5}=2x-1}\end{array}\right.$,
∵${(\sqrt{{4x}^{2}+6x-5})}^{2}{=(2x+1)}^{2}$,
∴4x2+6x-5=4x2+4x+1,
∴2x=6,
解得x=3,
经检验x=3是原方程的解,
∴方程$\sqrt{4{x}^{2}+6x-5}$+$\sqrt{4{x}^{2}-2x-5}$=4x的解是:x=3.
故答案为:x=±$\sqrt{39}$.
点评 此题主要考查了二次根式在解方程中的应用,要熟练掌握,解答此题的关键是在解决实际问题的过程中能熟练应用有关二次根式的概念、性质和运算的方法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
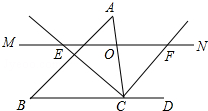 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
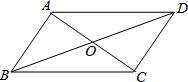 如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )| A. | ∠BAD=∠BCD,∠ABC=∠ADC | B. | OA=OC,OB=OD | ||
| C. | AD∥BC,AB=CD | D. | AC=BD,AD=CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com