练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．解方程
    （1）8（1-2x）3+27=0
    （2）（x+2）2=（1-2x）2．

    分析 （1）方程变形后，利用立方根定义开立方即可求出解；
    （2）利用两数的平方相等，两数相等或互为相反数求出解即可．

    解答 解：（1）方程整理得：（1-2x）3=-$\frac{27}{8}$，
    开立方得：1-2x=-$\frac{3}{2}$，
    解得：x=$\frac{5}{4}$；
    （2）方程变形得：x+2=1-2x或x+2=2x-1，
    解得：x=-$\frac{1}{3}$或x=3．

    点评 此题考查了解一元二次方程-因式分解法，以及立方根，熟练掌握解方程的方法是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    17．某广告公司欲招聘一名创作总监，对2名应试者进行了三项素质测试，他们的各项测试成绩如下表所示：
    应试者测试成绩
    创新能力计算机能力公关能力
     甲 72 50 88
     乙 85 74 45
    如果公司赋予“创新能力”、“计算机能力”、“公关能力”三项的权重为5：3：2，则本次招聘中应试者乙将被录用（填“甲”或“乙”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．解下列不等式（组），并把解集在数轴上表示出来：
    （1）$\left\{\begin{array}{l}{2x+6＞0}\\{1-2x≥0}\end{array}\right.$                    
    （2）1-$\frac{x+6}{2}$＜$\frac{2x+1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

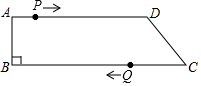    15．如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=30cm．点P从点A出发，以1cm/s的速度向点D移动，点Q从点C出发，以3cm/s的速度向点B运动，点P和点Q分别从点A和点C同时出发，移动时间为ts．规定若其中一个动点先到达端点（终点）时，另一个动点也随之停止运动．
    （1）求时间t的取值范围；
    （2）当四边形ABQP为矩形时，求时间t的值；
    （3）是否存在时间t的值，使得△APQ的面积是△ABC的面积的一半？若存在，请求出t的值，若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．某工厂甲、乙两名工人参加操作技能培训，现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次，记录如下：
    甲8588848583
    乙8387848685
    （1）请你分别计算这两组数据的平均数；
    （2）现要从中选派一人参加操作技能比赛，从统计学的角度考虑，你认为选派哪名工人参加合适？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

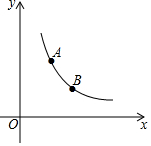    12．如图，已知点A（1，a）与点B（b，1）在反比例函数y=$\frac{2}{x}$（x＞0）图象上，点P（m，0）是x轴上的任意一点，若△PAB的面积为2，此时m的值是-1或7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知抛物线y=ax2+x+c（a≠0）经过点A（-1，0），B（2，0）两点，与y轴相交于点C，点D为抛物线的顶点．
    （1）求抛物线的解析式及点D的坐标；
    （2）△ABC的外接圆与抛物线的另一交点为E，直接写出E点的坐标；
    （3）记△ABC得外接圆圆心为M，求圆心M的坐标；
    （4）在x轴上有一点P，且∠EBO+∠MPO=α，当tanα=3时，求OP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，已知在平面直角坐标系xOy中，O为坐标原点，点A，B分别在x轴上（点A在原点左侧，点B在原点右侧），OB=4OA，经过点A，B的抛物线交y轴于点C（0，2），且∠ACB=90°．
    （1）求抛物线的解析式；
    （2）点N为该抛物线第一象限上一点，满足∠NOC=∠CBO，联结BN，NO，求△BON的面积；
    （3）点D为抛物线对称轴上一点，且在x轴下方，点E在y轴负半轴上，当以B，E，D为顶点的三角形与△ABC相似时（∠DBE与∠ABC为对应角），求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解方程组$\left\{\begin{array}{l}{x+2y=1}\\{3x-4y=13}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案