
【题目】如图,D、B、C三点在同一条直线上,∠C=50°,∠FBC=80°.问:∠DBF的平分线BE与AC有怎样的位置关系?并说明理由.
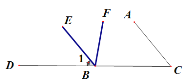
解:BE与AC一定平行.
∵D、B、C三点在同一条直线上,
∴∠DBF+∠FBC=180°( ).
又∵∠FBC=80°(已知).
∴∠DBF= .
又∵BE平分∠DBF(已知).
∴![]() ( ).
( ).
又∵∠C=50°(已知),
∴∠ =∠ ( ),
∴ ∥ .( )
科目:初中数学 来源: 题型:
【题目】4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了两幅不完整统计图(每组包括最小值不包括最大值).九年级(1)班每天阅读时间在0.5小时以内的学生占全班人数的8%.根据统计图解答下列问题:
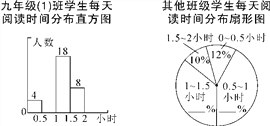
(1)九年级(1)班有 名学生;
(2)补全直方图;
(3)除九年级(1)班外,九年级其他班级每天阅读时间在1~1.5小时的学生有165人,请你补全扇形统计图;
(4)求该年级每天阅读时间不少于1小时的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
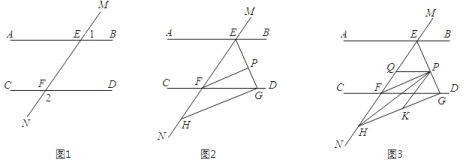
【题目】如图 1,直线 MN 与直线 AB,CD 分别交于点 E,F,∠1 与∠2 互补.
(1)试判断直线 AB 与直线 CD 的位置关系,并说明理由;
(2)如图 2,∠BEF 与∠EFD 的角平分线交于点 P,EP 与 CD 交于点 G,点 H 是 MN 上一点,且GH⊥EG,求证:PF∥GH;
(3)如图 3,在(2)的条件下,连结 PH,在 GH 上取一点 K,使得∠PKG=2∠HPK,过点 P 作 PQ 平分∠EPK 交 EF 于点 Q,问∠HPQ 的大小是否发生变化?若不变,请求出其值;若变化,说明理由.(温馨提示:三角形的三个内角和为 180°)
查看答案和解析>>
科目:初中数学 来源: 题型:
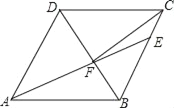
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的有几个( )
.其中一定成立的有几个( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是三边都不相等的三角形,点O和点P是这个三角形内部两点.
(1)如图①,如果点P是这个三角形三个内角平分线的交点,那么∠BPC和∠BAC有怎样的数量关系?请说明理由;
(2)如图②,如果点O是这个三角形三边垂直平分线的交点,那么∠BOC和∠BAC有怎样的数量关系?请说明理由;
(3)如图③,如果点P(三角形三个内角平分线的交点),点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部,那么∠BPC和∠BOC有怎样的数量关系?请直接回答.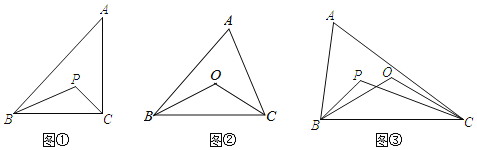
查看答案和解析>>
科目:初中数学 来源: 题型:
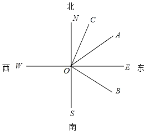
【题目】如图,直线SN为南北方向,OB的方向是南偏东60°,∠SOB与∠NOC互余,OA平分∠BON.
(1)射线OC的方向是 .
(2)求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
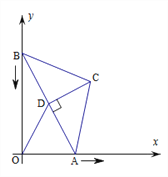
【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动
(1)连接OC,线段OC的长随t的变化而变化,当OC最大时,t=____;
(2)当△ABC的边与坐标轴平行时,t=____。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是5,b与c之间的距离是7,则正方形ABCD的面积是( )
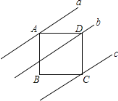
A.70B.74C.144D.148
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com