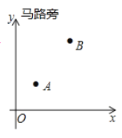
【题目】要在马路边设一个共享单车投放点，向
两家公司提供服务，投放点应设在什么地方，才能使从到它的距离之和最短？小明根据实际情况，以马路为
轴建立了如图所示的平面直角坐标系，
点的坐标为
，
点的坐标为
，则从两点到投放点距离之和的最小值是__________，投放点的坐标是__________．
轻巧夺冠周测月考直通高考系列答案科目：初中数学 来源： 题型：
【题目】如图所示，长方形纸片ABCD的长AD＝9cm，宽AB＝3cm，将其折叠，使点D与点B重合．
求：（1）折叠后DE的长；（2）以折痕EF为边的正方形面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（5，0）两点，直线y＝﹣
x+3与y轴交于点C，与x轴交于点D．点P是直线CD上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E，设点P的横坐标为m．
(1)求抛物线的解析式；
(2)求PE的长最大时m的值．
(3)Q是平面直角坐标系内一点，在(2)的情况下，以PQCD为顶点的四边形是平行四边形是否存在？若存在，直接写出点Q的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，为了躲避台风，一轮船一直由西向东航行，上午
点，在
处测得小岛
的方向是北偏东
，以每小时
海里的速度继续向东航行，中午
点到达
处，并测得小岛的方向是北偏东
，若小岛周围
海里内有暗礁，问该轮船是否能一直向东航行？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现阅读下面的材料，然后解答问题：
截长补短法，是初中数学几何题中一种常见辅助线的做法．在证明线段的和、差、倍、分等问题中有着广泛的应用．截长法：在较长的线段上截一条线段等于较短线段，而后再证明剩余的线段与另一段线段相等．补短法：就是延长较短线段与较长线段相等，而后证延长的部分等于另一条线段．
请用截长法解决问题（1）
（1）已知：如图1等腰直角三角形
中，
，
是角平分线，交
边于点
．求证：
．
请用补短法解决问题（2）
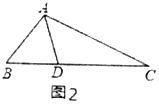
（2）如图2，已知，如图2，在
中，
，是的角平分线．求证：．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
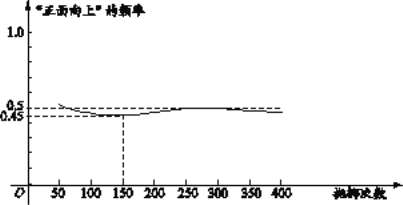
下面有三个推断：
①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；
②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；
③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.45．
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为更新果树品种，某果园计划新购进
、
两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中种苗的单价为8元/棵，购买种苗所需费用
（元）与购买数量
（棵）之间存在如图所示的函数关系．
（1）求与的函数关系式；
（2）若在购买计划中，种苗的数量不超过35棵，但不少于种苗数量的一半，请设计购买方案，使总费用最低，并求出最低费用．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l1：y1=x和直线l2：y2=﹣2x+6相交于点A，直线l2与x轴交于点B，动点P沿路线O→A→B运动．
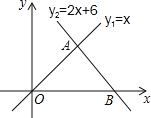
（1）求点A的坐标，并回答当x取何值时y1＞y2？
（2）求△AOB的面积；
（3）当△POB的面积是△AOB的面积的一半时，求出这时点P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
