
 ��ͼ����M������ABCD��ƽ��ֱ������ϵ�У���M������Ϊ��3��-1������A������Ϊ��-2��$\sqrt{3}$������B������Ϊ��-3��0������C��x���ϣ��ҵ�D�ڵ�A����࣮
��ͼ����M������ABCD��ƽ��ֱ������ϵ�У���M������Ϊ��3��-1������A������Ϊ��-2��$\sqrt{3}$������B������Ϊ��-3��0������C��x���ϣ��ҵ�D�ڵ�A����࣮���� ��1�����ݹ��ɶ��������εı߳�Ϊ2�����Կɵ��ܳ�Ϊ8��
��2������ͼ2���ȸ���������EF�ij�����EE'-FE'=EF=7����ʽ�ã�3t-2t=7���ɵ�t��ֵ��
�������EBA=60�㣬���FBA=120�㣬�ٵá�MBF=45�㣬��ӿɵã���MBD=��MBF+��FBD=45��+60��=105�㣻
��3��������������ۣ���������MN��ME��
��һ���������ͼ5�ɾ���Ϊ1��֪��BDΪ��M�����ߣ���BC�ǡ�M�����ߣ��á�MBE=30�㣬��ʽΪ3t+$\sqrt{3}$=2t+6��������ɣ�
�ڶ����������ͼ6��ͬ���ɵ�t��ֵ��
���  �⣺��1����ͼ1����A��AE��BC��E��
�⣺��1����ͼ1����A��AE��BC��E��
�ߵ�A������Ϊ��-2��$\sqrt{3}$������B������Ϊ��-3��0����
��AE=$\sqrt{3}$��BE=3-2=1��
��AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{��\sqrt{3}��^{2}+{1}^{2}}$=2��
���ı���ABCD�����Σ�
��AB=BC=CD=AD=2��
������ABCD���ܳ�=2��4=8��
��2������ͼ2����M��x����е�ΪF��BC���е�ΪE��
��M��3��-1����
��F��3��0����
��BC=2����EΪBC���е㣬
��E��-4��0����
��EF=7��
��EE'-FE'=EF��
��3t-2t=7��
t=7��
���ɣ�1����֪��BE=1��AE=$\sqrt{3}$��
��tan��EBA=$\frac{AE}{BE}$=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$��
���EBA=60�㣬
��ͼ4�����FBA=120�㣬
���ı���ABCD�����Σ�
���FBD=$\frac{1}{2}$��FBA=$\frac{1}{2}��120��$=60�㣬
��BC�ǡ�M�����ߣ�
��MF��BC��
��F��BC���е㣬
��BF=MF=1��
���BFM�ǵ���ֱ�������Σ�
���MBF=45�㣬
���MBD=��MBF+��FBD=45��+60��=105�㣻
��3������BM����M��MN��BD������ΪN����ME��BC��E��
��һ���������ͼ5��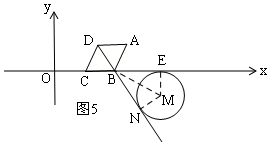
���ı���ABCD�����Σ���ABC=120�㣬
���CBD=60�㣬
���NBE=60�㣬
�ߵ�M��BD���ڵ�ֱ�ߵľ���Ϊ1��
��MN=1��
��BDΪ��M�����ߣ�
��BC�ǡ�M�����ߣ�
���MBE=30�㣬
��ME=1��
��EB=$\sqrt{3}$��
��3t+$\sqrt{3}$=2t+6��
t=6-$\sqrt{3}$��
�ڶ����������ͼ6�����ı���ABCD�����Σ���ABC=120�㣬
���DBC=60�㣬
���NBE=120�㣬
�ߵ�M��BD���ڵ�ֱ�ߵľ���Ϊ1��
��MN=1��
��BDΪ��M�����ߣ�
��BC�ǡ�M�����ߣ�
���MBE=60�㣬
��ME=MN=1��
��Rt��BEM��tan60��=$\frac{ME}{BE}$��
EB=$\frac{1}{tan60��}$=$\frac{\sqrt{3}}{3}$��
��3t=2t+6+$\frac{\sqrt{3}}{3}$��
t=6+$\frac{\sqrt{3}}{3}$��
��������������M��BD���ڵ�ֱ�ߵľ���Ϊ1ʱ��t=6-$\sqrt{3}$��6+$\frac{\sqrt{3}}{3}$��
���� �������ı��κ�Բ���ۺ��⣬���������ε����ʡ�Բ�����ߵ����ʺ��ж�����������Ǻ���ֵ������ֱ�������ε����ʡ������˶����⣬��������Ƚϸ��ӣ�Ū�嶯���˶������ٶȡ�ʱ���·�̵Ĺ�ϵ�����뷽�����ϣ��ҵ�����ϵ�����ʱ��t��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����һ�������������ͼ������ͼ����ʾ���ݼ������������IJ�����ǣ�������
��ͼ����һ�������������ͼ������ͼ����ʾ���ݼ������������IJ�����ǣ�������| A�� | �� | B�� | 2�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ѧ����ʦ��ѧ����������һ�����⣺̽������y=$\frac{x}{x+1}$��ͼ�������ʣ�С�����ѧϰ�����ľ��飬�Ժ���y=$\frac{x}{x+1}$��ͼ�������ʽ�����̽����������С���̽�����̣�����������ɣ�
��ѧ����ʦ��ѧ����������һ�����⣺̽������y=$\frac{x}{x+1}$��ͼ�������ʣ�С�����ѧϰ�����ľ��飬�Ժ���y=$\frac{x}{x+1}$��ͼ�������ʽ�����̽����������С���̽�����̣�����������ɣ�| x | �� | -5 | -4 | -3 | -2 | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | 1 | 2 | m | 4 | 5 | �� |
| y | �� | $\frac{5}{4}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | ��2 | �� 3 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{4}{5}$ | $\frac{5}{6}$ | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ֱ��y1=kx+$\sqrt{2}$�뷴��������y2=$\frac{{2\sqrt{2}}}{x}$��ͼ���ڵ�A��B����������ֱ���C��D���㣬��AC=CD��
ֱ��y1=kx+$\sqrt{2}$�뷴��������y2=$\frac{{2\sqrt{2}}}{x}$��ͼ���ڵ�A��B����������ֱ���C��D���㣬��AC=CD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪AB��CF��DE��CF��DE��BC���ڵ�P������ABC=70�㣬��CDE=130�㣮
��ͼ����֪AB��CF��DE��CF��DE��BC���ڵ�P������ABC=70�㣬��CDE=130�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com