
分析 本题可设共有x个小朋友,则水彩笔有4x+48个,令其<6(x-1)+4,令其≥6(x-1)+1,化解不等式组得出x的取值范围,则x即为其中的最小的整数.
解答 解:设共有x个小朋友,则水彩笔有4x+48个.
∵最后一个小朋友不足4件,
∴4x+48<6(x-1)+4,
∵最后一个小朋友最少1件,
∴4x+48≥6(x-1)+1,
联立得$\left\{\begin{array}{l}{4x+48<6(x-1)+4}\\{4x+48≥6(x-1)+1}\end{array}\right.$,
解得25<x≤26.5.
∵x取正整数26,
∴水彩笔为4x+48=152.
故答案为:152.
点评 本题考查的是一元一次不等式的运用,要注意解不等式时不等号两边同时除以一个负数,不等式方向要改变.


科目:初中数学 来源: 题型:解答题
 如图,已知数轴上的点A对应的数为6,B是数轴上的一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿着数轴向左匀速运动,设运动时间为t秒(t>0).
如图,已知数轴上的点A对应的数为6,B是数轴上的一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿着数轴向左匀速运动,设运动时间为t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
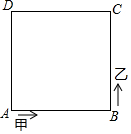 如图所示,甲、乙两人同时沿着边长为100m的正方形广场ABCD,按A→B→C→D→A…的顺序跑,甲从A出发,速度为82m/min,乙从B出发,速度为90m/min,则当乙第二次追到甲时,他在正方形广场的( )
如图所示,甲、乙两人同时沿着边长为100m的正方形广场ABCD,按A→B→C→D→A…的顺序跑,甲从A出发,速度为82m/min,乙从B出发,速度为90m/min,则当乙第二次追到甲时,他在正方形广场的( )| A. | AB边 | B. | BC边 | C. | CD边 | D. | AD边 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com