Question

19．两个大小不同的等腰直角三角形三角板如图①所示放置，图②是由它抽象出的几何图形B，C，E在同一条直线上，连结DC．
（1）请找出图②中的全等三角形，并给予说明（注意：结论中不得含有未标识的字母）；
（2）请判断DC与BE的位置关系，并证明；
（3）若CE=2，BC=4，求△DCE的面积．

Answer 1

分析 （1）根据等腰直角三角形的性质可以得出△ABE≌△ACD；
（2）由△ABE≌△ACD可以得出∠AEB=∠ADC，进而得出∠AEC=90°，就可以得出结论；
（3）根据三角形的面积公式即可得到结论．

解答 解：（1）△ABE≌△ACD，
∵△ABC和△ADE是等腰直角三角形，
∴AB=AC，AE=AD，∠BAC=∠EAD=90°，
∴∠BAC+∠EAC=∠DAE+∠EAC，
∴∠BAE=∠CAD，
在△ABE和△ACD中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AE=AD}\end{array}\right.$
∴△ABE≌△ACD（SAS）．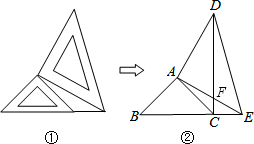

（2）∵△ABE≌△ACD，
∴∠AEB=∠ADC．
∵∠ADC+∠AFD=90°，
∴∠AEB+∠AFD=90°．
∵∠AFD=∠CFE，
∴∠AEB+∠CFE=90°，
∴∠FCE=90°，
∴DC⊥BE；

（3）∵CE=2，BC=4，
∴BE=6，
∵△ABE≌△ACD，
∴CD=BE=6，
∴△DCE的面积=$\frac{1}{2}$CE•CD=$\frac{1}{2}$×2×6=6．

点评 本题考查了等腰直角三角形的性质的运用，全等三角形的判定及性质的运用，垂直的判定的运用，解答时证明三角形全等是关键．