
分析 ①将(1,0)点代入函数,解出k的值即可作出判断;
②首先考虑,函数为一次函数的情况,从而可判断为假;
③根据②即可作出判断;
④当k=0时,函数为一次函数,无最大之和最小值,当k≠0时,函数为抛物线,求出顶点的纵坐标表达式,即可作出判断.
解答 解:①将(1,0)代入可得:2k-(4k+1)-k+1=0,解得:k=0,此选项正确.
②当k=0时,y=-x+1,该函数的函数值y始终随x的增大而减小;此选项正确;
③y=-x+1,经过3个象限,此选项错误;
④当k=0时,函数无最大、最小值;k≠0时,y最=-$\frac{24{k}^{2}+1}{8k}$,当k>0时,有最小值,最小值为负;当k<0时,有最大值,最大值为正;此选项正确.
正确的是①②④.
故答案为:①②④.
点评 此题考查二次函数的性质,一次函数的性质,利用举特例的方法是解决问题常用方法.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{8}{27}$的立方根是±$\frac{2}{3}$ | B. | -125没有立方根 | ||
| C. | -1的平方的立方根是1 | D. | $\root{3}{9}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
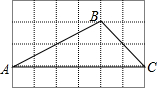 如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+7)(x-8)=x2+x-56 | B. | (x+2)2=x2+4 | ||
| C. | (7-2x)(8+x)=56-2x2 | D. | (3x+4y)(3x-4y)=9x2-16y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com