
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.

【答案】(1)见解析;(2) 猜想:DM=AM. 理由见解析.
【解析】
(1)根据等边三角形的性质得出相等的角,相等的边,再等量代换即可得证;
(2)根据题意画出图形,根据轴对称的性质,得∠MDC=∠EDC,DE=DM,然后根据(1)的结论和等边三角形的性质证明即可.
(1)证明:∵△ABC是等边三角形,∴∠BAC=∠ACB=60°.
又∵∠BAD+∠DAC=∠BAC,∠EDC+∠DEC=∠ACB,
∴∠BAD+∠DAC=∠EDC+∠DEC.
∵DE=DA,∴∠DAC=∠DEC,
∴∠BAD=∠EDC.
(2)解:按题意画图如图所示.

猜想:DM=AM.
理由如下:∵点M、E关于直线BC对称,
∴∠MDC=∠EDC,DE=DM.
又由(1)知∠BAD=∠EDC,∴∠MDC=∠BAD.
∵∠ADC=∠BAD+∠B,即∠ADM+∠MDC=∠BAD+∠B,
∴∠ADM=∠B=60°.
又∵DA=DE=DM,
∴△ADM是等边三角形,
∴DM=AM.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点H,点G在弧BD上,连接AG,交CD于点K,过点G的直线交CD延长线于点E,交AB延长线于点F,且EG=EK. 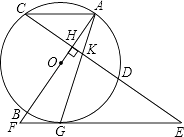
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为13,CH=12,AC∥EF,求OH和FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘载重480 t的船,容积是1050 m3,现有甲种货物450 m3,乙种货物350 t,而甲种货物每吨体积2.5 m3,乙种货物每立方米0.5 t.问两种货物是否都能装上船? 如果不能,请说明理由,并求出为了最大限度地利用船的载重量和容积,两种货物应各装多少吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
A.( ![]() ,1)
,1)
B.(1,﹣ ![]() )
)
C.(2 ![]() ,﹣2)
,﹣2)
D.(2,﹣2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
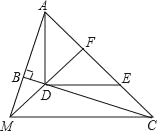
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD、AB的延长线相交于点M,连接MC.
(1)求证:∠FMC=∠FCM;
(2)将条件中的AD⊥DE与(1)中的结论互换,其他条件不变,命题是否正确?请给出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明本学期的数学测验成绩如表所示:
测验 类别 | 平时测验 | 期中 测验 | 期末 测验 | |||
第1次 | 第2此 | 第3次 | 第4次 | |||
成绩 | 80 | 86 | 84 | 90 | 90 | 95 |
(1)求六次测验成绩的众数和中位数;
(2)求小明本学期的数学平时测验的平均成绩;
(3)如果本学期的总评成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照3:3:4的比例计算所得,计算小明本学期学科的总评成绩。
查看答案和解析>>
科目:初中数学 来源: 题型:
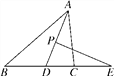
【题目】如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E,当P点在线段AD上运动时,∠E与∠B,∠ACB的数量关系为________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com