
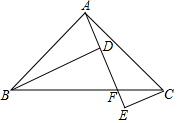
 如图,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,AE与BC交于F点.
如图,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,AE与BC交于F点.分析 (1)根据垂直的定义得到∠ADB=∠E=90°,根据余角的性质即可得到结论;
(2)根据余角和补角的性质即可得到结论.
解答 解:(1)∵BD⊥AE于D,CE⊥AE于E,
∴∠ADB=∠E=90°,
∴∠ABD+∠BAD=∠ECF+∠EFC=90°,
∴∠ABD与∠BAD,∠ECF与∠EFC互余,
故答案为:∠ABD与∠BAD,∠ECF与∠EFC;
(2)图中与∠BAD相等的角是∠ABD,∠CAE,∠ABD;
∵∠BAC=∠ADB=90°,
∴∠BAD+∠ABD=∠BAD+∠CAE=90°,
∴图中与∠BAD相等的角是∠ABD,∠CAE,
∴∠EAC=∠ABD,
故答案为:∠ABD,∠CAE;∠ABD.
点评 本题考查了余角与补角,熟记余角与补角的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
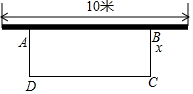 如图,某中学准备用铁栅栏围建一个长方形的花圃ABCD,且使花圃的面积为40平方米,其中靠墙的边为AB,已知墙的长度为10米,设BC的长为x米,DC的长为y米
如图,某中学准备用铁栅栏围建一个长方形的花圃ABCD,且使花圃的面积为40平方米,其中靠墙的边为AB,已知墙的长度为10米,设BC的长为x米,DC的长为y米查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+1 | B. | $\sqrt{a+1}$ | C. | a2+1 | D. | $\sqrt{{a}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
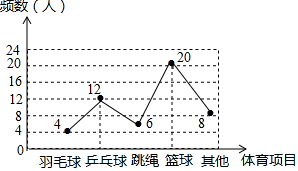 体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )| A. | 16% | B. | 24% | C. | 30% | D. | 40% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 28 | B. | 30 | C. | 45 | D. | 53 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com