
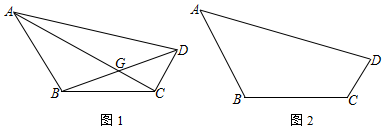
分析 (1)根据等腰三角形ABC的顶角求得底角的度数,即可得出∠ACD=90°;
(2)先过点B作BE⊥AC于E,则∠AEB=90°,∠ABE=60°,设CD=1,则AB=BC=k,根据∠BAE=30°,求得CG=$\frac{1}{5}$AC=$\frac{1}{5}\sqrt{3}$k,EG=AG-AE=$\frac{3}{10}\sqrt{3}$k,再根据△BEG∽△DCG,得出$\frac{EG}{CG}$=$\frac{BE}{DC}$,即$\frac{\frac{3}{10}\sqrt{3}k}{\frac{1}{5}\sqrt{3}k}$=$\frac{\frac{1}{2}k}{1}$,解方程求得k=3即可;
(3)先根据∠BAP=∠DPC,∠B=∠C=120°,判定△ABP∽△PCD,得到$\frac{PC}{AB}=\frac{CD}{BP}$,再设CD=1,BP=x,则AB=BC=k,PC=k-x,进而得出$\frac{k-x}{k}=\frac{1}{x}$,即x2-kx+k=0,要使点P是唯一的,则方程x2-kx+k=0有两个相等的实数根,据此得出△=k2-4k=0,求得k=4.
解答 解:(1)∵∠ABC=∠BCD=120°,AB=BC,
∴△ABC中,∠ACB=$\frac{1}{2}$(180°-120°)=30°,
∴∠ACD=∠BCD-∠ACB=120°-30°=90°,
∴AC⊥CD;
(2)如图1,过点B作BE⊥AC于E,则∠AEB=90°,∠ABE=60°,
∴∠BAE=30°,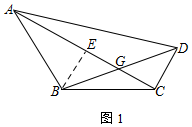
∴Rt△ABE中,BE=$\frac{1}{2}$AB,AE=CE=$\sqrt{3}$BE,
设CD=1,则AB=BC=k,
∴BE=$\frac{1}{2}$k,AE=$\frac{1}{2}\sqrt{3}$k=CE,
∴AC=$\sqrt{3}$k,
又∵AG=4GC,
∴AG=$\frac{4}{5}$AC=$\frac{4}{5}\sqrt{3}$k,CG=$\frac{1}{5}$AC=$\frac{1}{5}\sqrt{3}$k,
∴EG=AG-AE=$\frac{4}{5}\sqrt{3}$k-$\frac{1}{2}\sqrt{3}$k=$\frac{3}{10}\sqrt{3}$k,
∵BE∥CD,
∴△BEG∽△DCG,
∴$\frac{EG}{CG}$=$\frac{BE}{DC}$,即$\frac{\frac{3}{10}\sqrt{3}k}{\frac{1}{5}\sqrt{3}k}$=$\frac{\frac{1}{2}k}{1}$,
化简,得$\frac{3}{2}$=$\frac{1}{2}$k,
∴k=3;
(3)如图2,∵∠APD=120°,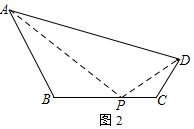
∴∠APB+∠DPC=60°,
又∵∠B=120°,
∴∠APB+∠BAP=60°,
∴∠BAP=∠DPC,
又∵∠B=∠C=120°,
∴△ABP∽△PCD,
∴$\frac{PC}{AB}=\frac{CD}{BP}$,
设CD=1,BP=x,则AB=BC=k,PC=k-x,
∴$\frac{k-x}{k}=\frac{1}{x}$,即x2-kx+k=0,
要使点P是唯一的,则方程x2-kx+k=0有两个相等的实数根,
∴△=k2-4k=0,
解得k=4或0,
又∵k>0,
∴k=4.
点评 本题属于四边形综合题,主要考查了相似三角形的判定与性质,等腰三角形的性质以及一元二次方程根与系数的关系的综合应用,解决问题的关键是作辅助线构造相似三角形和直角三角形,运用相似三角形的对应边成比例以及勾股定理进行计算求解.解题时注意:一元二次方程ax2+bx+c=0(a≠0),当△=0时,方程有两个相等的两个实数根.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (15x2y-5xy2)÷5xy=3x-5y | B. | 98×102=(100-2)(100+2)=9996 | ||
| C. | $\frac{x}{x+3}-1=\frac{3}{x+3}$ | D. | (3x+1)(x-2)=3x2+x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-2(x+1)2 | B. | y=-2(x-1)2 | C. | y=-2x2+1 | D. | y=-2x2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com