
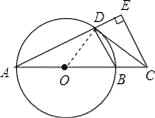
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.

【答案】(1)证明过程见解析;(2)6.
【解析】试题分析:(1)连接OD,由CD是⊙O切线,得到∠ODC=90°,根据AB为⊙O的直径,得到∠ADB=90°,等量代换得到∠BDC=∠ADO,根据等腰直角三角形的性质得到∠ADO=∠A,即可得到结论;(2)根据垂直的定义得到∠E=∠ADB=90°,根据平行线的性质得到∠DCE=∠BDC,根据相似三角形的性质得到![]() ,解方程即可得到结论.
,解方程即可得到结论.
试题解析:(1)连接OD, ∵CD是⊙O切线, ∴∠ODC=90°, 即∠ODB+∠BDC=90°,
∵AB为⊙O的直径, ∴∠ADB=90°, 即∠ODB+∠ADO=90°, ∴∠BDC=∠ADO,
∵OA=OD, ∴∠ADO=∠A, ∴∠BDC=∠A;
(2)∵CE⊥AE, ∴∠E=∠ADB=90°, ∴DB∥EC, ∴∠DCE=∠BDC, ∵∠BDC=∠A, ∴∠A=∠DCE,
∵∠E=∠E, ∴△AEC∽△CED, ∴![]() , ∴EC2=DEAE, ∴16=2(2+AD), ∴AD=6.
, ∴EC2=DEAE, ∴16=2(2+AD), ∴AD=6.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
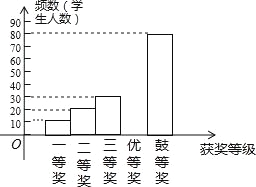
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= ,b= ,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=4S△ADF.其中正确的有( )
AE2;④S△ABC=4S△ADF.其中正确的有( )
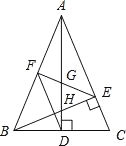
A.1个 B.2 个 C.3 个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
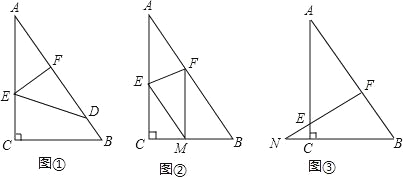
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若点A (a,﹣b)在第一象限内,则点B (a,b﹣3)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com