
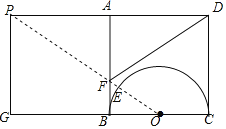
【题目】如图,已知正方形ABCD的边长为4,点E是正方形内都一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为__.

【答案】2![]() -2
-2
【解析】
根据正方形的性质得到∠ABC=90°,推出∠BEC=90°,得到点E在以BC为直径的半圆上移动,如图,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,连接PO交AB于F,交⊙O于E,则线段EP的长即为FD+FE的长度最小值,根据勾股定理即可得到结论.
解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵∠ABE=∠BCE,
∴∠BCE+∠CBE=90°,
∴∠BEC=90°,
∴点E在以BC为直径的半圆上移动,
如图,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,
连接PO交AB于F,交半圆O于E,则线段EP的长即为FD+FE的长度最小值,OE=4,
∵∠G=90°,PG=BG=AB=4,
∴OG=6,
∴OP=![]() =
=![]() ,
,
∴EP=![]() -2,
-2,
∴FD+FE的长度最小值为![]() -2,
-2,
故答案为:2![]() -2.
-2.


科目:初中数学 来源: 题型:
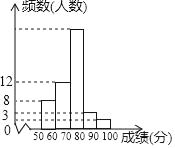
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 购买江苏省体育彩票有“中奖”与“不中奖”两种情况,所以中奖的概率是![]()
B. 国家级射击运动员射靶一次,正中靶心是必然事件
C. 如果在若干次试验中一个事件发生的频率是![]() ,那么这个事件发生的概率一定也是
,那么这个事件发生的概率一定也是![]()
D. 如果车间生产的零件不合格的概率为![]() ,那么平均每检查1000个零件会查到1个次品
,那么平均每检查1000个零件会查到1个次品
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.

(Ⅰ)如图①,若∠BAC=250,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为10的⊙O经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+48=0的两根.
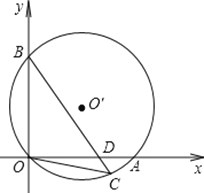
(1)求线段OA、OB的长;
(2)已知点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求C点的坐标;
(3)在⊙O上是否存在点P,使S△POD=S△ABD.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
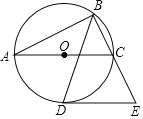
【题目】如图,以△ABC的边AC为直径的O恰为△ABC的外接圆,∠ABC的平分线交O于点D,过点D作DE∥AC交BC的延长线于点E
(1)求证:DE是⊙O的切线;
(2)若AB=4![]() ,BC=2
,BC=2![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
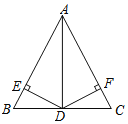
【题目】在△ABC中,AB=AC,点D为边BC上一点,且AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:BE=CF;
(2)若∠B=40°,求∠ADF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快5G网络建设,某移动通信公司在山顶上建了一座5G信号通信塔AB,山高BE=100米(A,B,E在同一直线上),点C与点D分别在E的两侧(C,E,D在同一直线上),BE⊥CD,CD之间的距离1000米,点D处测得通信塔顶A的仰角是30°,点C处测得通信塔顶A的仰角是45°(如图),则通信塔AB的高度约为( )米.(参考数据:![]() ,
,![]() )
)
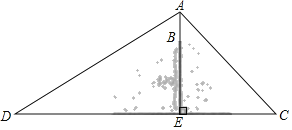
A.350B.250C.200D.150
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com