
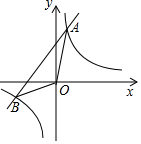
 如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根
如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根| K | 1 | 2 | 3 | … | n(n为正整数) |
| A点的横坐标 | 1 | 1 | 1 | … | 1 |
| B点的横坐标 | -2 | -3 | -4 | … | -n-1 |
分析 (1)根据k的值,即可得到一元二次方程的解,进而得到A点的横坐标,B点的横坐标;
(2)根据当k=n(n为正整数)时,A点的横坐标为1,B点的横坐标为-n-1,可得A(1,n+1),B(-n-1,-1),运用待定系数法即可得出直线AB的解析式;
(3)先求得直线AB与y轴交于(0,n),再根据当Sn=40时,$\frac{1}{2}$×n(n+1+1)=40,即可得到n=8,进而得出A(1,9),据此可得双曲线的解析式为:y=$\frac{9}{x}$.
解答 解:(1)当k=1时,方程x2+x-2=0的解为:x1=1,x2=-2;
当k=2时,方程x2+2x-3=0的解为:x1=1,x2=-3;
k=3时,方程x2+3x-4=0的解为:x1=1,x2=-4;
k=n时,方程x2+nx-n-1=0的解为:x1=1,x2=-n-1;
∵点A在第一象限,点B在第三象限,
∴A点的横坐标依次为:1,1,1,…,1;
B点的横坐标依次为:-2,-3,-4,…,-n-1;
故答案为:1,1,1,…,1;-2,-3,-4,…,-n-1;
(2)当k=n(n为正整数)时,A点的横坐标为1,B点的横坐标为-n-1,
令x=1,则y=$\frac{n+1}{1}$=n+1;
令x=-n-1,则y=$\frac{n+1}{-n-1}$=-1;
∴A(1,n+1),B(-n-1,-1),
设直线AB的解析式为y=px+q,则
$\left\{\begin{array}{l}{n+1=p+q}\\{-1=(-n-1)p+q}\end{array}\right.$,
解得$\left\{\begin{array}{l}{p=1}\\{q=n}\end{array}\right.$,
∴直线AB的解析式为y=x+n;
(3)∵直线y=x+n中,令x=0,则y=n,即直线AB与y轴交于(0,n),
∴当Sn=40时,$\frac{1}{2}$×n(n+1+1)=40,
解得n=8(负值已舍去),
∴A(1,9),
∴双曲线的解析式为:y=$\frac{9}{x}$.
点评 本题主要考查了一次函数与反比例函数交点问题以及一元二次方程的解,解题时注意:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+2015)2+2016 | B. | y=(x-2015)2+2016 | C. | y=-(x-2015)2-2016 | D. | y=-(x+2015)2+2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
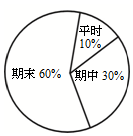 小明同学八年级上学期的数学成绩记录如表:
小明同学八年级上学期的数学成绩记录如表:| 测验类别 | 平时测验 | 期中考试 | 期末考试 | |||
| 测验1 | 测验2 | 测验3 | 课题学习 | |||
| 成绩 | 88 | 72 | 86 | 98 | 90 | 84 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com