
 为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:
为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:| 课外作业时间 (分组) | 人数 (频数) |
| 30~45 | 5 |
| 45~60 | 12 |
| 60~75 | a |
| 75~90 | 10 |
| 90~105 | b |
分析 (1)由 45~60的人数及其百分比可得总人数,总人数乘以60~75的百分比可得a的值,根据各分组人数之和等于总数可得b的值;
(2)用360°乘以75~90min的部分的人数所占比例即可;
(3)根据频数分布直方图的作图可得.
解答 解:(1)本次调查共抽取了12÷24%=50名学生,
则a=50×40%=20,b=50-(5+12+20+10)=3,
故答案为:50,20,3;
(2)360°×$\frac{10}{50}$=72°,
答:作业时间为75~90min的部分对应的扇形圆心角的度数为72°;
(3)如下图所示: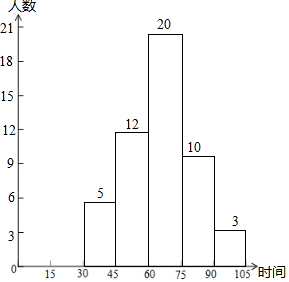
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
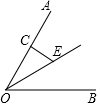 如图,∠AOB=60°,点E在∠AOB的平分线上,EC⊥OA,且CE=1,点D是OB上的一个动点,当ED取最小值时,线段CD的长度为$\sqrt{3}$.
如图,∠AOB=60°,点E在∠AOB的平分线上,EC⊥OA,且CE=1,点D是OB上的一个动点,当ED取最小值时,线段CD的长度为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左平移4单位 | B. | 向右平移4单位 | C. | 向左平移8单位 | D. | 向右平移8单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)完成下面的证明.
(1)完成下面的证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-$\sqrt{3}$x+$\frac{1}{2}$=0 | B. | x2+$\sqrt{3}$x+$\frac{1}{2}$=0 | C. | x2-$\sqrt{3}$x+1=0 | D. | x2+$\sqrt{3}$x-$\frac{1}{2}$=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com