
 ,最小底长为
,最小底长为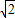 ,然后根据面积来进行判断即可,此种情况下方案较多,只要符合题意即可.
,然后根据面积来进行判断即可,此种情况下方案较多,只要符合题意即可.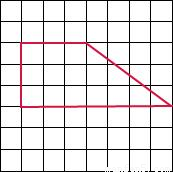
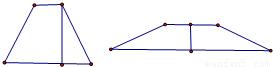
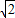 ,下底3
,下底3 ,高2
,高2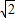 ;
;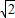 ,下底6
,下底6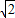 ,高
,高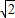 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 (2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.
(2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
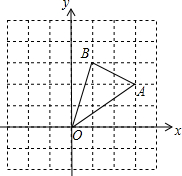 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1 OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1 OB1.查看答案和解析>>
科目:初中数学 来源: 题型:
 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个长方形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个长方形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com