
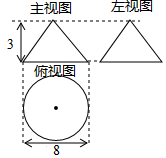
 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是( )
已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是( )| A. | 40π | B. | 24π | C. | 20 π | D. | 12π |
分析 先利用三视图得到底面圆的半径为4,圆锥的高为3,再根据勾股定理计算出母线长l为5,然后根据圆锥的侧面积公式:S侧=πrl代入计算即可.
解答 解:根据三视图得到圆锥的底面圆的直径为8,即底面圆的半径r为4,圆锥的高为3,
所以圆锥的母线长l=$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以这个圆锥的侧面积是π×4×5=20π.
故选C.
点评 本题考查了圆锥的计算,连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.连接顶点与底面圆心的线段叫圆锥的高.圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.掌握圆锥的侧面积公式:S侧=$\frac{1}{2}$•2πr•l=πrl是解题的关键.也考查了三视图.


科目:初中数学 来源: 题型:解答题
 如图,已知直线l1:y=-2x+8与双曲线C:y=$\frac{6}{x}$(x>0),相交于点A和B(点A在点B的左上方),直线l2:y=kx(k>0)与直线l1相交于点C,于双曲线C相交于点D.(1)求点A、B的坐标;
如图,已知直线l1:y=-2x+8与双曲线C:y=$\frac{6}{x}$(x>0),相交于点A和B(点A在点B的左上方),直线l2:y=kx(k>0)与直线l1相交于点C,于双曲线C相交于点D.(1)求点A、B的坐标;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②④ | C. | ①② | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小于0 | B. | 等于0 | ||
| C. | 大于0 | D. | 与a,b,c,d的取值有关 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A、B、C、D、E的坐标分别是(0,a)、(-3,2)、(b,m)、(-b,m),则点E的坐标是( )
如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A、B、C、D、E的坐标分别是(0,a)、(-3,2)、(b,m)、(-b,m),则点E的坐标是( )| A. | (2,-3) | B. | (2,3) | C. | (3,2) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| … | 0 | 50 | 200 | … | |
| y | … | 1 | -1 | 1 | … |
| A. | x1=x2=100 | B. | x1=0,x2=200 | C. | x1=50,x2=150 | D. | x1=50,x2=250 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com