
| A. | $\frac{3b}{15a}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a-b}$ | C. | $\frac{{x}^{2}}{3x}$ | D. | $\frac{{x}^{2}+y2}{x+y}$ |
分析 最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答 解:A、$\frac{3b}{15a}=\frac{b}{5a}$,故本选项错误;
B、$\frac{{a}^{2}-{b}^{2}}{a-b}=a+b$,故本选项错误;
C、$\frac{{x}^{2}}{3x}=\frac{x}{3}$,故本选项错误;
D、分子、分母都不能再分解,且不能约分,是最简分式.故本选项正确;
故选D
点评 本题考查了最简分式的定义.分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
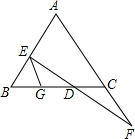 如图,已知EG∥AF,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只需写出一种情况)
如图,已知EG∥AF,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只需写出一种情况)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com