
| 卖出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量P(件) | 500 | 490 | 480 | 470 | … |
分析 (1)根据表格中数据的特点易知p与x成一次函数关系,设出p=kx+b,从表格中任取两点坐标,利用待定系数法确定出k与b的值,进而得到p与x的函数关系式;
(2)根据销售利润=(每件的售价-每件的进价)×销售量,可得y=px-40p,化简即可得到利润的关系式;
解答 解:p与x成一次函数关系.设函数关系式为p=kx+b,
则 $\left\{\begin{array}{l}{500=50k+b}\\{490=51k+b}\end{array}\right.$,
解得:k=-10,b=1000,
∴p=-10x+1000,
经检验可知:当x=52,p=480,当x=53,p=470时也适合这一关系式,
∴所求的函数关系为p=-10x+1000;
当x=60时,p=-10×60+1000=400,
故答案为:p=-10x+1000,400.
点评 此题考查了一次函数及二次函数的图象与性质,第一问猜想p与x成一次函数关系式,利用待定系数法确定出关系式后不要忘了验证;第三问求最值问题时,应根据第二问得到的函数表达式,利用二次函数性质来求解.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
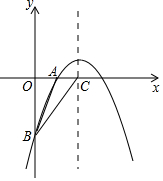 如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
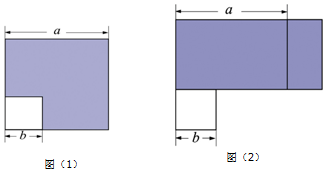
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(千瓦时)的函数图象是一条折线,根据图象解下列问题:
如图,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(千瓦时)的函数图象是一条折线,根据图象解下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com