Question

当x＝2时，抛物线y＝ax²＋bx＋c取得最小值－1，并且抛物线与y轴交于点C（0，3），与x轴交于点A、B．

（1）求该抛物线的关系式；

（2）若点M（x，y₁），N（x＋1，y₂）都在该抛物线上，试比较y₁与y₂的大小；

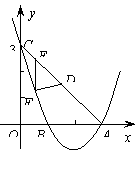
（3）D是线段AC的中点，E为线段AC上一动点（A、C两端点除外），过点E作y轴的平行线EF与抛物线交于点F．问：是否存在△DEF与△AOC相似？若存在，求出点E的坐标；若不存在，则说明理由．

 

Answer 1

解：（1）由题意可设抛物线的关系式为y＝a(x－2)²－1       

因为点C（0，3）在抛物线上

所以3＝a(0－2)²－1，即a＝1          

所以，抛物线的关系式为y＝(x－2)²－1＝x²－4 x＋3

（2）∵点M（x，y₁），N（x＋1，y₂）都在该抛物线上

∴y₁－y₂＝（x²－4 x＋3）－[(x＋1)²－4(x＋1)＋3]＝3－2 x

当3－2 x＞0，即时，y₁＞y₂        

当3－2 x＝0，即时，y₁＝y₂        

当3－2 x＜0，即时，y₁＜y₂        

（3）令y＝0，即x²－4 x＋3＝0，得点A（3,0），B（1,0），线段AC的中点为D（,）

直线AC的函数关系式为y＝－x＋3

因为△OAC是等腰直角三角形，所以，要使△DEF与△OAC相似，△DEF也必须是等腰直角三角形．由于EF∥OC，因此∠DEF＝45°，所以，在△DEF中只可能以点D、F为直角顶点．

①当F为直角顶点时，DF⊥EF，此时△DEF∽△ACO，DF所在直线为

由，解得，（舍去）

将代入y＝－x＋3，得点E（，）

②当D为直角顶点时，DF⊥AC，此时△DEF∽△OAC，由于点D为线段AC的中点，因此，DF所在直线过原点O，其关系式为y＝x．

解x²－4 x＋3＝x，得，（舍去）

将代入y＝－x＋3，得点E（，）      …………12分