
 某渔船在海面A处,看见北偏东30°方向距离10$\sqrt{3}$海里处有一灯塔C,北偏西75°方向距离15$\sqrt{6}$海里处有一灯塔B,渔船由A向正北航行到D,再看灯塔船B在南偏西60°方向,问灯塔C与D相距多少海里?在D的什么方向?
某渔船在海面A处,看见北偏东30°方向距离10$\sqrt{3}$海里处有一灯塔C,北偏西75°方向距离15$\sqrt{6}$海里处有一灯塔B,渔船由A向正北航行到D,再看灯塔船B在南偏西60°方向,问灯塔C与D相距多少海里?在D的什么方向? 分析 作AE⊥BD于E,CF⊥AD于F,根据题意求出∠B的度数,根据正弦的概念求出AE的长,得到AD的长,根据直角三角形的性质求出DF、CF的长,得到答案.
解答 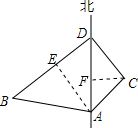 解:作AE⊥BD于E,CF⊥AD于F,
解:作AE⊥BD于E,CF⊥AD于F,
由题意得,AB=15$\sqrt{6}$海里,AC=10$\sqrt{3}$海里,∠BAD=75°,∠ADB=60°,
则∠B=45°,
∴AE=$\frac{\sqrt{2}}{2}$×AB=15$\sqrt{3}$海里,
∵∠ADB=60°,
∴∠DAE=30°,
∴AD=30,
∵∠DAC=30°,AC=10$\sqrt{3}$海里,
∴CF=$\frac{1}{2}$AC=5$\sqrt{3}$海里,AF=15海里,
∴DF=15海里,又FC=5$\sqrt{3}$海里,
∴CD=$\sqrt{C{F}^{2}+D{F}^{2}}$=10$\sqrt{3}$海里,
则∠CDF=30°,
∴灯塔C与D相距10$\sqrt{3}$海里,C在D南偏东30°方向.
点评 本题考查的是解直角三角形的应用-方向角问题,正确作出辅助线、构造直角三角形、灵活运用三角函数的概念是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com