
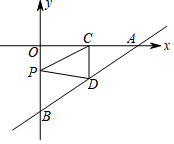
 如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )| A. | (0,-1) | B. | (0,-2) | C. | (0,-3) | D. | (0,-4) |
分析 根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,(方法一)结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标;(方法二)由点D、D′关于y轴对称,可得出点P为线段CD′的中点,根据中点坐标公式即可得出点P的坐标.
解答 解:作点D关于y轴的对称点D′,连接CD′交y轴于点P,此时PC+PD取最小值,如图所示.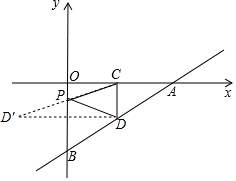
当x=0时,y=$\frac{2}{3}$x-4=-4,
∴点B的坐标为(0,-4);
当y=$\frac{2}{3}$x-4=0时,x=6,
∴点A的坐标为(6,0).
∵点C、D分别是线段OA、AB的中点,
∴点C的坐标为(3,0),点D的坐标为(3,-2).
∵点D、D′关于y轴对称,
∴点D′的坐标为(-3,-2).
(方法一)设直线CD′的解析式为y=kx+b,
将C(3,0)、D′(-3,-2)代入y=kx+b,
$\left\{\begin{array}{l}{3k+b=0}\\{-3k+b=-2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=-1}\end{array}\right.$,
∴直线CD′的解析式为y=$\frac{1}{3}$x-1.
当x=0时,y=$\frac{1}{3}$x-1=-1,
∴点P的坐标为(0,-1).
(方法二)∵点D、D′关于y轴对称,
∴点P为线段CD′的中点,
∴点P的坐标为(0,-1).
故选A.
点评 本题考查了一次函数图象上点的坐标特征以及轴对称中的最短路线问题,根据两点之间线段最短找出当PC+PD取最小值时点P的位置是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:解答题
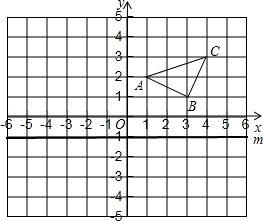 如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).
如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤$\frac{6}{5}$ | B. | x<2 | C. | x$<\frac{6}{5}$ | D. | x≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对旅客上飞机前的安检 | |
| B. | 了解全班同学每周体育锻炼的时间 | |
| C. | 选出某校短跑最快的学生参加全市比赛 | |
| D. | 了解某批次灯泡的使用寿命情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-250,-100) | B. | (100,250) | C. | (-100,-250) | D. | (250,100) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第7个菱形的边长是27.
如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第7个菱形的边长是27.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com