
分析 (1)首先去掉括号,再合并同类项,然后把x=-2代入,求出算式5(x2-2)-2(2x2+4)的值是多少即可.
(2)把y=2x+1代入y=3x2+3x-1,求出x的值是多少,进而求出y的值,确定出直线y=2x+1与抛物线y=3x2+3x-1的交点坐标即可.
解答 解:(1)5(x2-2)-2(2x2+4)
=5x2-10-4x2-8
=x2-18
=(-2)2-18
=4-18
=-14
(2)把y=2x+1代入y=3x2+3x-1,
可得3x2+x-2=0,
解得x=$\frac{2}{3}$或x=-1,
①当x=$\frac{2}{3}$时,
y=2×$\frac{2}{3}$+1
=$\frac{4}{3}+1$
=2$\frac{1}{3}$
②当x=-1时,
y=2×(-1)+1
=-2+1
=-1
所以直线y=2x+1与抛物线y=3x2+3x-1的交点坐标是($\frac{2}{3},2\frac{1}{3}$)、(-1,-1).
点评 (1)此题主要考查了整式的化简求值问题,解答此题的关键是注意去括号时符号的变化.
(2)此题还考查了直线与抛物线的交点坐标的求法,采用代入法即可.


科目:初中数学 来源: 题型:选择题
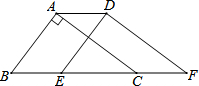 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论:
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,折线ABC是在某市乘出租车需付车费y(元)与行车里程x(千米)之间的函数关系图象.若某人付费30.8元,出租车行驶了多少千米?
如图所示,折线ABC是在某市乘出租车需付车费y(元)与行车里程x(千米)之间的函数关系图象.若某人付费30.8元,出租车行驶了多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
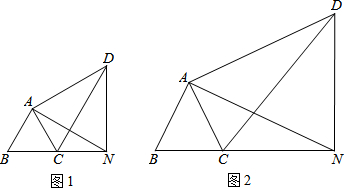
 如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F是线段AD上的三等分点,连接BE、CE、BF、CF,若$\frac{BC}{AD}=\frac{2}{3}$,且BC=4a.
如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F是线段AD上的三等分点,连接BE、CE、BF、CF,若$\frac{BC}{AD}=\frac{2}{3}$,且BC=4a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
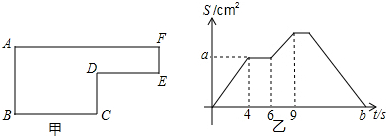
| A. | 图1中BC的长是4厘米 | B. | 图2中的a是12 | ||
| C. | 图1中的图形面积是60平方厘米 | D. | 图2中的b是19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com