
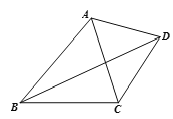
【题目】如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠DCB=123°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠DAC的度数为_________度.
【答案】58°
【解析】
延长![]() 和
和![]() ,过
,过![]() 点作
点作![]() 于
于![]() 点,过D店作
点,过D店作![]() 于F点,根据BD是
于F点,根据BD是![]() 的平分线可得出
的平分线可得出![]() ,∠DBC=25°;过D作
,∠DBC=25°;过D作![]() 于G点,可得出
于G点,可得出![]() ,进而得出CD为∠ACF的平分线和已知条件得到AD为
,进而得出CD为∠ACF的平分线和已知条件得到AD为![]() 的平分线;再结合∠DCB=123°,确定∠ACB=66°,最后根据三角形的外角的定义得到∠ACF=116°,然后根据CD为∠ACF的平分线求得.
的平分线;再结合∠DCB=123°,确定∠ACB=66°,最后根据三角形的外角的定义得到∠ACF=116°,然后根据CD为∠ACF的平分线求得.
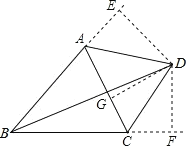
解:延长BA和BC,过D点做![]() 于E点,过D店做
于E点,过D店做![]() 于F点,
于F点,
![]() 是
是![]() 的平分线
的平分线
∴![]() =25°
=25°
![]() ,
,
又![]()
![]()
![]() ,
,
![]() 为
为![]() 的平分线,
的平分线,
![]() .
.
在![]() 与
与![]() 中,
中,
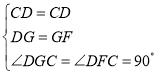
![]()
![]() 为∠ACF的平分线
为∠ACF的平分线
∴∠DCF=∠DCG
又∵∠DCB=123°
∴![]()
∴∠DCF=∠DCG=57°
∴∠ACB=123°-57°=66°,
在![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
又∵![]() =
=![]()
![]() =58°.
=58°.
故答案为:58°.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】1.概念学习.已知![]() ,点
,点![]() 为其内部一点,连接
为其内部一点,连接![]() 、
、![]() 、
、![]() ,在
,在![]() 、
、![]() 、
、![]() 中,如果存在一个三角形,其内角与
中,如果存在一个三角形,其内角与![]() 的三个内角分别相等,那么就称点
的三个内角分别相等,那么就称点![]() 为
为![]() 的等角点.
的等角点.

2.理解应用
(1)判断以下两个命题是否为真今题,若为真令题,则在相应横线内写“真命题”;反之,则写“假命题”.
①内角分别为![]() 、
、![]() 、
、![]() 的三角形存在等角点; ;
的三角形存在等角点; ;
②任意的三角形都存在等角点; ;
(2)如图①,点![]() 是锐角
是锐角![]() 的等角点,若
的等角点,若![]() ,探究图①中,
,探究图①中,![]() 、
、![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
3.解决问题
如图②,在![]() 中,
中,![]() ,若
,若![]() 的三个内角的角平分线的交点
的三个内角的角平分线的交点![]() 是该三角形的等角点,求
是该三角形的等角点,求![]() 三角形三个内角的度数.
三角形三个内角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两种不同的数对处理器![]() 、
、![]() .当数对
.当数对![]() 输入处理器
输入处理器![]() 时,输出数对
时,输出数对![]() ,记作
,记作![]() ,
,![]() ,
,![]() ;但数对
;但数对![]() 输入处理器
输入处理器![]() 时,输出数对
时,输出数对![]() ,记作
,记作![]() ,
,![]() ,
,![]() .
.
(1)![]() ,
,![]() ( , ),
( , ),![]() ,
,![]() ( , ).
( , ).
(2)当![]() ,
,![]() ,
,![]() 时,求
时,求![]() ,
,![]() ;
;
(3)对于数对![]() ,
,![]() ,
,![]() ,
,![]() 一定成立吗?若成立,说明理由;若不成立,举例说明.
一定成立吗?若成立,说明理由;若不成立,举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
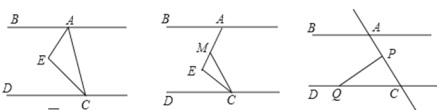
【题目】如图 ,CE 平分∠ACD,AE 平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
(2)如图,在(1)的结论下,当∠E=90°保持不变时,移动直角顶点 E,使∠MCE=∠ECD, 当直角顶点 E 点移动时,请确定∠BAE 与![]() ∠MCD 的数量关系,并说明理由;
∠MCD 的数量关系,并说明理由;
(3)如图,在(1)的结论下,P 为线段 AC 上的一个定点,点 Q 为直线 CD 上的一个动点,当点 Q 在射线 CD 上运动时(点 C 除外)∠BAC 与∠CPQ+∠CQP 有何数量关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习三角形的知识时, 发现如下三个有趣的结论:
(1)如图①, ∠A=∠C=90°, ∠ABC的平分线与∠ADC的平分线交于点E, 则BE、DE的位置关系是 ;
(2)如图②, ∠A=∠C=90°, BE平分∠ABC, DF平分∠ADC的外角, 则BE与DF的位置关系是 ;
(3)如图③, ∠A=∠C=90°, ∠ABC的外角平分线与∠ADC的外角平分线交于点E, 则BE、DE的位置关系是 . 请你完成命题 (3)证明.
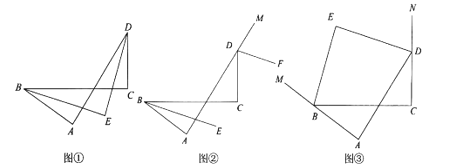
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任刘老师对全班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)八年级(3)班学生总人数是 ,并将条形统计图补充完整;
(2)刘老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这些学生中任意挑选两名担任活动记录员,请用列表或画树状图的方法,求恰好选中1名男生和1名女生担任活动记录员的概率.
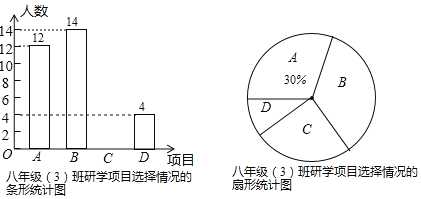
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com