
| 电器类型 | 进价(元)/台 | 售价(元)/台 |
| 甲 | 1500 | 1900 |
| 乙 | 1800 | 2400 |
分析 (1)根据题意和表格中的数据可以求得总利润y(元)与购进甲型电器x(台)的函数解析式;
(2)根据(1)中的函数解析式可以得到相应的不等式,从而可以求得至少要购进多少台乙型电器.
解答 解:(1)由题意可得,
y=(1900-1500)x+(2400-1800)(100-x)=-200x+60000,
答:所获总利润y(元)与购进甲型电器x(台)的函数解析式是y=-200x+60000;
(2)由题意可得,
-200x+60000≥55000,
解得,x≤25,
∴100-x≥75,
答:至少要购进75台乙型电器.
点评 本题考查一次函数的应用、一元一次不等式的应用,解答本题的关键是明确题意,求出相应的函数解析式和列出相应的不等式,利用一次函数的性质和不等式的性质解答.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:选择题
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
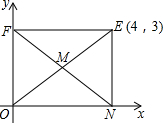 【阅读】
【阅读】查看答案和解析>>
科目:初中数学 来源: 题型:解答题
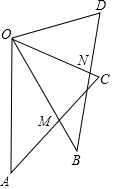 已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.
已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
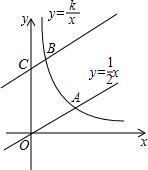 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移4个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,OA=3BC.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移4个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,OA=3BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com