考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,解一元二次方程-配方法,解一元二次方程-公式法
专题:计算题
分析:(1)利用直接开平方法求解即可;
(2)先求出x2,再利用直接开平方法求解即可;
(3)把(x+5)看作一个整体,利用直接开平方法求解即可;
(4)把(3-x)看作一个整体,利用直接开平方法求解即可;
(5)利用因式分解法求解即可;
(6)提取公因式(2x-1),利用因式分解法求解即可;
(7)利用因式分解法求解即可;
(8)利用因式分解法求解即可.
解答:解:(1)∵(±8)
2=64,
∴x=±8,
即x
1=8,x
2=-8;
(2)移项得,5x
2=
,
系数化为1得,x
2=
,
x=±
,
即x
1=
,x
2=-
;
(3)x+5=±4,
x
1=-1,x
2=-9;
(4)移项,系数化为1得,(3-x)
2=9,
3-x=±3,
即x
1=6,x
2=0;
(5)移项得,3y
2-2y=0,
y(3y-2)=0,
∴y=0,3y-2=0,
解得y
1=0,y
2=
;
(6)(2x-1)(2+x)=0,
∴2x-1=0,2+x=0,
解得x
1=
,x
2=-2;
(7)移项得,3x(x+2)-5(x+2)=0,
(x+2)(3x-5)=0,
∴x+2=0,3x-5=0,
解得x
1=-2,x
2=
;
(8)(3y-1)(3y-1+2)=0,
∴3y-1=0,3y+1=0,
解得y
1=
,y
2=-
.
点评:本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.



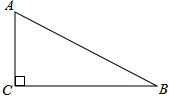 如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm.以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm.以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是( )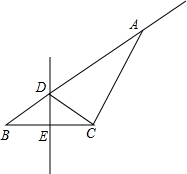 如图,在△ABC中,DE是边BC的垂直平分线,与边AB、BC交于点D、E,如果△ACD的周长为17cm,△ABC的周长为25cm,根据这些条件,你可以求出哪些线段的长?
如图,在△ABC中,DE是边BC的垂直平分线,与边AB、BC交于点D、E,如果△ACD的周长为17cm,△ABC的周长为25cm,根据这些条件,你可以求出哪些线段的长?
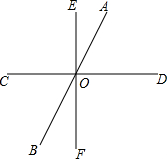 如图,直线AB、CD、EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,
如图,直线AB、CD、EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,