Question

9．如图，将一张三角形形纸片剪成四个小三角形，然后将其中的一个小三角形再按同样的方法剪成四个小三角形，…，如此循环进行下去．

（1）填表：

次数	1	2	3	4	…
个数	4	7	①10	②13	…

（2）填空：剪n次，共剪出（3n+1）个三角形．
（3）能否经过若干次分割后共得到2016片纸片？若能，请直接写出相应的次数；若不能，请说明理由．

Answer 1

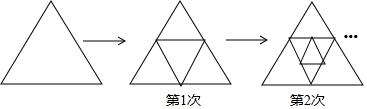
分析 根据图跟表我们可以看出n代表所剪次数，a_n代表小正三角形的个数，不难发现：多剪一次，多3个三角形，由此可求出剪n次时正三角形的个数．

解答 （1）由题可得：多剪一次，多3个三角形，
∴7+3=10，10+3=13，
故答案为：10，13；

（2）由图可知，没剪的时候，有一个三角形，以后每剪一次就多出三个，
故第一次操作后，三角形共有1+3=4个；
第二次操作后，三角形共有1+3×2=7个；
第三次操作后，三角形共有1+3×3=10个；
…
∴第n次操作后，三角形共有1+3×n=（3n+1）个；
故答案为：3n+1；

（3）不能．
理由：当3n+1=2016时，解得n=671$\frac{2}{3}$，
∵n不是整数，
∴不能．

点评 此类题属于图形变化类的规律型问题，解决问题的关键是找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．