
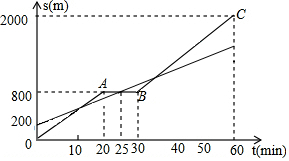
 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.分析 (1)根据函数图象可以分别求得小明各段对应的函数解析式,从而可以解答本题;
(2)根据函数图象可以求得小明爸爸对应的函数解析式,从而可以求得小明出发多少时间与爸爸第三次相遇;
(3)根据(2)中小明爸爸对应的函数解析式可以求得小明爸爸到达公园用的时间,从而可以得到小明在步行过程中停留的时间需作怎样的调整.
解答 解:(1)设小明在OA段对应的函数解析式为s=k1t,
800=k1×20,得k1=40,
即小明在OA段对应的函数解析式为s=20t,
由图象可知小明在OB段对应的函数解析式为:s=800,
设小明在BC段对应的函数解析式为:s=k2t+b2,
$\left\{\begin{array}{l}{30{k}_{2}+{b}_{2}=800}\\{60{k}_{2}+{b}_{2}=2000}\end{array}\right.$,得$\left\{\begin{array}{l}{{k}_{2}=40}\\{{b}_{2}=-400}\end{array}\right.$,
即小明在BC段对应的函数解析式为:s=40t-400,
由上可得,小明所走路程s与时间t的函数关系式是:s=$\left\{\begin{array}{l}{40t}&{(0≤t≤20)}\\{800}&{(20<t≤30)}\\{40t-400}&{(30<t≤60)}\end{array}\right.$;
(2)设小明的爸爸所走路程s与时间t的函数关系式是s=k3t+b3,
$\left\{\begin{array}{l}{{b}_{3}=200}\\{25{k}_{3}+{b}_{3}=800}\end{array}\right.$,得$\left\{\begin{array}{l}{{k}_{3}=24}\\{{b}_{3}=200}\end{array}\right.$,
即小明的爸爸所走路程s与时间t的函数关系式是s=24t+200,
∴$\left\{\begin{array}{l}{s=24t+200}\\{s=40t-400}\end{array}\right.$,得$\left\{\begin{array}{l}{t=37.5}\\{s=1100}\end{array}\right.$,
即小明出发37.5min时与爸爸第三次相遇;
(3)当s=2000时,2000=24t+200,得t=75,
∵75-60=15,
∴小明希望比爸爸早18min到达公园,则小明在步行过程中停留的时间需要缩短3min.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用数形结合的思想解答.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
 如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,连接EF,将△AEF绕点A逆时针旋转45°,使E落在E1,F落在F1,连接BE1并延长交DF1于点G,如果AB=2$\sqrt{2}$,AE=1,则DG=$\frac{4\sqrt{5}}{5}$.
如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,连接EF,将△AEF绕点A逆时针旋转45°,使E落在E1,F落在F1,连接BE1并延长交DF1于点G,如果AB=2$\sqrt{2}$,AE=1,则DG=$\frac{4\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
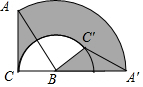 如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )| A. | 4π+2$\sqrt{3}$ | B. | $\frac{16}{3}$π-2$\sqrt{3}$ | C. | $\frac{16}{3}$π+2$\sqrt{3}$ | D. | 4π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
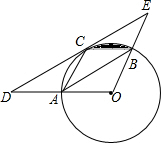 如图,?AOBC的顶点A、B、C在⊙O上,过点C作DE∥AB交OA延长线于D点,交OB延长线于点E.
如图,?AOBC的顶点A、B、C在⊙O上,过点C作DE∥AB交OA延长线于D点,交OB延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
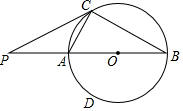 在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.
在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com