
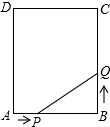
 如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别是从A、B同时出发,
如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别是从A、B同时出发,分析 (1)设xs后,△PBQ的面积等于9cm2,根据${S_{△PBQ}}=\frac{1}{2}PB•BQ$,列方程求解可得;
(2)由PB2+BQ2=PQ2得(6-x)2+(2x)2=52,即可判断;
(3)由S五边形APQCD=S矩形ABCD-S△PBQ=AB•BC-$\frac{1}{2}$PB•BQ=72-6x+x2=(x-3)2+63,即可得答案.
解答 解:(1)设xs后,△PBQ的面积等于9cm2,
此时,AP=xcm,PB=(6-x)cm,BQ=2xcm.
由${S_{△PBQ}}=\frac{1}{2}PB•BQ$,得 $9=\frac{1}{2}(6-x)•2x$.
解得 x1=x2=3.
答:3秒后,△PBQ的面积等于9平方厘米;
(2)点P与点Q之间的距离不可能为5厘米.
由PB2+BQ2=PQ2得(6-x)2+(2x)2=52,
整理,得 5x2-12x+11=0,
容易判断此方程无实数根.
答:点P与点Q之间的距离不可能为5厘米;
(3)由S五边形APQCD=S矩形ABCD-S△PBQ
=AB•BC-$\frac{1}{2}$PB•BQ
=6×12-$\frac{1}{2}$×(6-x)•2x
=72-6x+x2
=(x-3)2+63,
∵(x-3)2≥0,
∴当x-3=0时,即(x-3)2的值为0时是最小值,
∴当x=3时,(x-3)2+63有最小值,此时为63.
答:3秒后,五边形APQCD的面积最小,最小值是63cm2.
点评 本题主要考查二次函数的应用,根据三角形的面积、勾股定理、五边形的面积列出方程或函数解析式是解题的关键.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
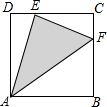 如图,正方形ABCD的边长为10,E是边DC上一点,F是边BC上一点,且DE=CF.问:当点E在什么位置时,△AEF的面积最小?最小面积是多少?
如图,正方形ABCD的边长为10,E是边DC上一点,F是边BC上一点,且DE=CF.问:当点E在什么位置时,△AEF的面积最小?最小面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
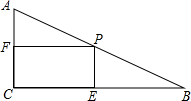 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,动点P从点B开始沿边BA以2cm/s的速度向点A移动,过点P作PE⊥BC,PF⊥AC,设点P移动的时间为t,四边形PECF的面积为S.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,动点P从点B开始沿边BA以2cm/s的速度向点A移动,过点P作PE⊥BC,PF⊥AC,设点P移动的时间为t,四边形PECF的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
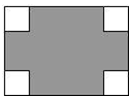 如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.
如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com