
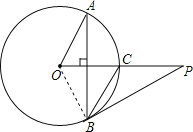
【题目】已知P是⊙O外一点,PO交⊙O于点C,OC=CP=2,弦AB⊥OC,∠AOC的度数为60°,连接PB.

(1)求BC的长;
(2)求证:PB是⊙O的切线.
【答案】(1)BC=2;(2)见解析
【解析】
试题分析:(1)连接OB,根据已知条件判定△OBC的等边三角形,则BC=OC=2;
(2)欲证明PB是⊙O的切线,只需证得OB⊥PB即可.
(1)解:如图,连接OB.
∵AB⊥OC,∠AOC=60°,
∴∠OAB=30°,
∵OB=OA,
∴∠OBA=∠OAB=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC的等边三角形,
∴BC=OC.
又OC=2,
∴BC=2;
(2)证明:由(1)知,△OBC的等边三角形,则∠COB=60°,BC=OC.
∵OC=CP,
∴BC=PC,
∴∠P=∠CBP.
又∵∠OCB=60°,∠OCB=2∠P,
∴∠P=30°,
∴∠OBP=90°,即OB⊥PB.
又∵OB是半径,
∴PB是⊙O的切线.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a>b,则下列式子正确的是( )
A. -2015a>-2015b B. 2015a<2015b
C. 2015-a>2015-b D. a-2015>b-2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )
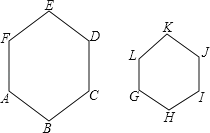
A.∠E=2∠K
B.BC=2HI
C.六边形ABCDEF的周长=六边形GHIJKL的周长
D.S六边形ABCDEF=2S六边形GHIJKL
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=![]() (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
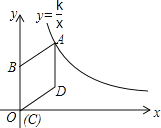
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=![]() (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com