
 在如图所示的直角坐标系中,菱形ABCD的边长是2,坐标系原点O为AB的中点,分别求点A,B,C,D的坐标.
在如图所示的直角坐标系中,菱形ABCD的边长是2,坐标系原点O为AB的中点,分别求点A,B,C,D的坐标. 分析 由菱形的边长为2,O为AB的中点,可求得A(-1,0)B(1,0),然后利用勾股定理求得OD的长,即可求得点D的坐标,又由CD=AB=2,即可求得点C的坐标.
解答 解:∵菱形的边长为2,O为AB的中点,
∴A(-1,0)B(1,0),
在直角三角形AOD中,AO=1,AD=2,由勾股定理得:DO=$\sqrt{{2^2}-1}=\sqrt{3}$,
∴D(0,$\sqrt{3}$)
∵CD=2,C到AB的距离等于AD=$\sqrt{3}$,
∴C(2,$\sqrt{3}$)
综上,A(-1,0)B(1,0)C(2,$\sqrt{3}$)D(0,$\sqrt{3}$).
点评 此题考查了菱形的性质以及勾股定理.注意掌握坐标与图形的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
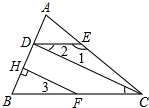 完成证明并写出推理根据:
完成证明并写出推理根据:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示.
某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的四边形是矩形 | B. | 对角线互相垂直的四边形是正方形 | ||
| C. | 平行四边形的对角线平分一组对角 | D. | 矩形的对角线相等且互相平分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com