
����Ŀ����![]() �У���
����![]() ��
��![]() ������ֱ���ϣ����
������ֱ���ϣ����![]() ��
��![]() ���غϣ�����
���غϣ�����![]() ��
��![]() ������ֱ���ϣ���
������ֱ���ϣ���![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��

��1����ͼ1����![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() ��
��![]() ���ϣ�����
���ϣ�����![]() ��
��![]() ��
��![]() ����˵����
����˵����![]() ��
��
ijͬѧ���ֿ�������������˼·��������⣺
˼·һ������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ����ͼ1
����ͼ1
��Ϊ![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() �ǵȱ�������
�ǵȱ�������
����![]() ����
����![]() ����
����![]()
��˵��![]() ����
����![]()
�ó�![]() ��
��
�Ӷ��õ����ۣ�
˼·��������![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����ͼ
����ͼ![]()
�������ڡ�˼·һ���е���������д���ɣ�
�ڸ��ݡ�˼·��������ʾ������д��˵�����̣�
��2����ͼ3����![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ����
����![]() ���߶�
���߶�![]() ���ӳ����ϣ�����
���ӳ����ϣ�����![]() ��
��![]() ��
��![]() ����̽��
����̽��![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
���𰸡���1���ٵ������������ߺ�һ��![]() ��
��![]() ���ڼ���������2��
���ڼ���������2��![]() ��������.
��������.
��������
��1���ٸ��ݵ��������ε����ʣ�ȫ�������ε��ж����ɽ�����⣮
��֤����DHA�ա�EMC��AAS�����Ƴ�AH=CM��DH=EM��֤����DHF�ա�EMF��AAS�����Ƴ�FM=FH=![]() HM�����ɽ�����⣮
HM�����ɽ�����⣮
��2�����ۣ�FH=![]() AC����ͼ3�У���DM��CA��CA ���ӳ�����M��֤����AMD�ա�CHE���Ƴ�AM=CH��DM=HE��֤����HFE�ա�MFD��AAS�����Ƴ�FH=FM=
AC����ͼ3�У���DM��CA��CA ���ӳ�����M��֤����AMD�ա�CHE���Ƴ�AM=CH��DM=HE��֤����HFE�ա�MFD��AAS�����Ƴ�FH=FM=![]() HM����.
HM����.
�⣺��1����˼·һ������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ����ͼ1
����ͼ1

��Ϊ![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() �ǵȱ�������
�ǵȱ�������
����![]() ����
����![]() ���������������ߺ�һ��
���������������ߺ�һ��
��˵��![]() ��
��![]()
�ó�![]()
�ʴ�Ϊ���������������ߺ�һ��![]() ��
��![]() ��
��
��˼·��������![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����ͼ2��
����ͼ2��

![]() �ǵȱ������Σ�
�ǵȱ������Σ�
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��2�����ۣ�![]() ��
��
���ɣ���ͼ3�У���![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ��
��

![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������֤��.
��֪����ͼ��![]() ��
��![]() .
.
��֤��![]() .
.
֤������![]() ��
��
��![]() __________��_______________________________________��.
__________��_______________________________________��.
��![]() ��_____________________________________________��.
��_____________________________________________��.
��![]() ��
��
��_______![]()
��![]() ��______________________________________��.
��______________________________________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�BC��6��AB��AC�Ĵ�ֱƽ���߷ֱ�BC�ڵ�M��N����MN��2�����AMN���ܳ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
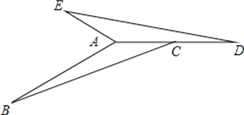
����Ŀ���ڡ�ABC�У���B+��ACB=30�㣬AB=4����ABC��ʱ����תһ���ǶȺ����ADE�غϣ��ҵ�Cǡ�ó�ΪAD�е㣬��ͼ
��1��ָ����ת���ģ��������ת�ǵĶ�����
��2�������BAE�Ķ�����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ӿ조��������ˮϵ��̬�������̡����ȣ���ˮ��������������10̨��ˮ�����豸������A��B�����ͺŵ��豸��ÿ̨�ļ۸�ֱ�Ϊa��Ԫ��b��Ԫ��ÿ�´�����ˮ���ֱ�Ϊ240�֣�200�֣���֪����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
��1����a��b��ֵ��
��2������Ԥ�㹺����ˮ�����豸���ʽ���105��Ԫ������Ϊ���ļ��ֹ�����
��3���ڣ�2���������£���ÿ��Ҫ������ˮ��������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ��ˮ���������һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ף��������������۹�˾���ݽ�������������ֱ���������ͼ��ʾ��ͳ��ͼ����2014��2018�꣬�����ҹ�˾�������������Ͽ����_____��˾(����������������)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
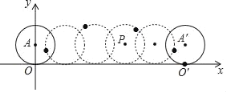
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��뾶Ϊ1��Բ��ԭ�������x�����������һ�ܣ�Բ��һ����ԭ��O�����O�䣬Բ��Ҳ�ӵ�A�����A�䣮
��1����O��������� ����A��������� ��
��2������P��Բ�ڹ���������Բ�ľ�����ijһλ�ã����Ե�P����O����O��Ϊ����������ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ![]() �еĵ�
�еĵ�![]() ������
������![]() ������Ϊ
������Ϊ![]() ���� ��
���� ��![]() ������ ��
Ϊ������ ��![]() ����Ƶ�
����Ƶ�![]() Ϊ��
Ϊ��![]() �ġ�
�ġ�![]() �������㡱 �� ���磺
�������㡱 �� ���磺![]() �ġ� 2 �������㡱Ϊ
�ġ� 2 �������㡱Ϊ![]() ����
����![]() ��
��
���� ��![]() �ġ� 3 �������㡱
�ġ� 3 �������㡱 ![]() ������Ϊ������
������������
���� ����![]() �ġ� 5 �������㡱
�ġ� 5 �������㡱 ![]() ������Ϊ
������Ϊ![]() �����
�����![]() �����ꣻ
�����ꣻ
���� ����![]() ��
��![]() ����������ϣ� ��
����������ϣ� ��![]() �ġ�
�ġ�![]() �������㡱Ϊ
�������㡱Ϊ![]() �㣬 ���߶�
�㣬 ���߶�![]() �ij���Ϊ�߶�
�ij���Ϊ�߶�![]() ���ȵ� 2 ���� ��
���ȵ� 2 ���� ��![]() ��ֵ ��
��ֵ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=k1x+b�뷴��������y=![]() ��x��0����ͼ����A��1��6����B��a��3�����㣮
��x��0����ͼ����A��1��6����B��a��3�����㣮

��1����k1��k2��ֵ��
��2�����ͼ��ֱ��д��k1x+b��![]() ��0��x��ȡֵ��Χ��
��0��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com