
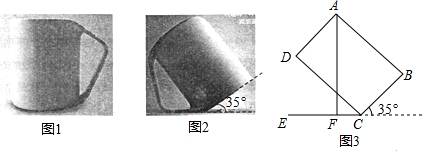
分析 (1)作BM⊥AF于M,BN⊥CF于N.由BM∥FN,推出∠MBC=∠BCN=35°,由题意∠ABM=90°-∠MBC=55°,推出∠FAB=90°-∠ABM=35°.
(2)分别在Rt△CBN,Rt△ABM中求出AM、BN即可解决问题.
解答 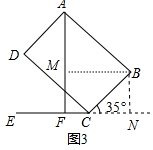 解:(1)作BM⊥AF于M,BN⊥CF于N.
解:(1)作BM⊥AF于M,BN⊥CF于N.
∵AF⊥EN,
∴∠MFN=∠BMF=∠BNF=90°,
∴四边形BMFN是矩形.
∴BM∥FN,
∴∠MBC=∠BCN=35°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABM=90°-∠MBC=55°,
∴∠FAB=90°-∠ABM=35°,
故答案为35°.
(2)在Rt△CBN中,∵BC=8,
∴FM=NB=BC•tan35°=0.5736×8≈4.59,
在Rt△ABM中,AM=AB•cos35°=10×0.8102≈8.20,
∴AF=AM+FM=8.20+4.59≈12.8(cm)
点评 本题考查解直角三角形的应用、矩形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,还在直角三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
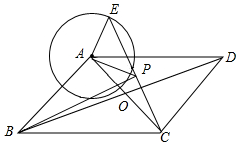 如图,?ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径为圆上一动点,连接CE,点P为CE的中点,连接BP,若AC=a,BD=b,则BP的最大值为( )
如图,?ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径为圆上一动点,连接CE,点P为CE的中点,连接BP,若AC=a,BD=b,则BP的最大值为( )| A. | $\frac{a}{2}$+1 | B. | $\frac{b}{2}$+1 | C. | $\frac{a+b}{2}$ | D. | $\frac{a+b}{2}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将直角三角形(其中∠B=30°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于120度.
如图,将直角三角形(其中∠B=30°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于120度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100 | B. | 120 | C. | 200 | D. | 220 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 85 | 90 | 90 | 85 |
| S2 | 1.0 | 1.0 | 1.2 | 1.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com