
【题目】公园内要铺设一段长方形步道,须用一些型号相同的灰色正方形地砖和一些型号相同 的白色等腰直角三角形地砖按如图所示方式排列.

(1) 若排列正方形地砖40块,则需使用三角形地砖____________块;
(2) 若排列三角形地砖2 020块,则需使用正方形地砖____________块.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=60°,将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方.

(1)在图1中,∠COM= 度;
(2)将图1中的三角板绕点O按逆时针方向旋转,使得ON在∠BOC的内部,如图2,若∠NOC=![]() ∠MOA,求∠BON的度数;
∠MOA,求∠BON的度数;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,当直线ON恰好平分∠BOC时,旋转的时间是 秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据二次函数y=ax2+bx+c(a≠0)的图象,有下列几种说法:
①a+b+c>0;
②该抛物线的对称轴是直线x=﹣1;
③当x=1时,y=2a;
④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
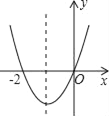
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
(部分参考数据:322=1024,522=2704,482=2304)
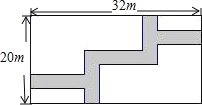
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用100厘米长的铅丝,弯折成一个长方形的模型.
(1)设长方形的面积为S平方厘米,长方形的长为![]() 厘米,用
厘米,用![]() 的式子表示S;
的式子表示S;
(2)当S=400平方厘米时,求![]() 的值;
的值;
(3)当S=625平方厘米时,求![]() 的值;
的值;
(4)S的值会不会为700平方厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京张高铁是2022年北京冬奥会的重要交通保障设施. 如图所示,京张高铁起自北京北站,途经清河、沙河、吕平等站,终点站为张家口南站,全长174千米.
(1)根据资料显示,京张高铁的客运价格拟定为0. 4元(人·千米),可估计京张高铁单程票价约为_________元(结果精确到个位);
(2)京张高铁建成后,将是世界上第一条设计时速为350千米/时的高速铁路. 乘高铁从北京到张家口的时间将缩短至1小时,如果按此设计时速运行,那么每站(不计起始站和终点站)停靠的平均时间是多少分钟?(结果保留整数)
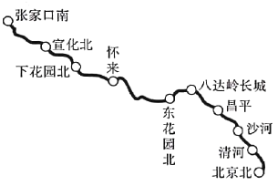
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…根据以上操作,若操作300次,得到小正方形的个数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么多少餐椅,到甲商场购买更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com