
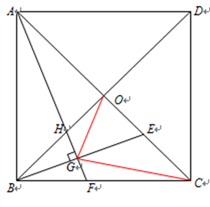
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交B0于H,连接OG,CC.
(1)求证:AH=BE;
(2)试探究:∠AGO的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】分析:(1)通过证明△AOH ≌ △BOE得到结论;
(2)易证△AOH∽△BGH得![]() ,由∠OHG =∠AHB可得△OHG∽△AHB,从而∠AGO=∠ABO=45°,从而可得结论;
,由∠OHG =∠AHB可得△OHG∽△AHB,从而∠AGO=∠ABO=45°,从而可得结论;
(3)易证△ABG ∽△BFG得![]() ,故AG·GF=BG 2 =5.再证明△AGO ∽△CGF.可得GO·CG =AG·GF=5.故S△OGC =
,故AG·GF=BG 2 =5.再证明△AGO ∽△CGF.可得GO·CG =AG·GF=5.故S△OGC =![]() CG·GO=
CG·GO=![]() .
.
详解:(1)∵四边形ABCD是正方形,
∴OA=OB,∠AOB=∠BOE=90°
∵AF⊥BE,
∴∠GAE+∠AEG=∠OBE+∠AEG=90°.
∴∠ GAE =∠OBE .
∴△AOH ≌ △BOE.
∴AH=BE .
(2)∵∠AOH=∠BGH=90°, ∠AHO=∠BHG,
∴△AOH∽△BGH.
∴![]() .
.
∴![]() .
.
∵∠OHG =∠AHB.
∴△OHG∽△AHB.
∴∠AGO=∠ABO=45°,即∠AGO的度数为定值.
(3)∵∠ABC=90°,AF⊥BE,
∴∠BAG=∠FBG,∠AGB=∠BGF=90°,
∴△ABG ∽△BFG.
∴![]() ,
,
∴AG·GF=BG 2 =5.
∵△AHB∽△OHG,
∴∠BAH=∠GOH=∠GBF.
∵∠AOB=∠BGF=90°,
∴∠AOG=∠GFC.
∵∠AGO=45°,CG⊥GO,
∴∠AGO=∠FGC=45°.
∴△AGO ∽△CGF.
∴![]() ,
,
∴GO·CG =AG·GF=5.
∴S△OGC =![]() CG·GO=
CG·GO=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 为常数).
为常数).
(1)当![]() ,
,![]() 时,求二次函数的最小值;
时,求二次函数的最小值;
(2)当![]() 时,若在函数值
时,若在函数值![]() 的情况下,只有一个自变量
的情况下,只有一个自变量![]() 的值与其对应,求此时二次函数的解析式;
的值与其对应,求此时二次函数的解析式;
(3)当![]() 时,若在自变量
时,若在自变量![]() 的值满足
的值满足![]() ≤
≤![]() ≤
≤![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 的最小值为21,求此时二次函数的解析式.
的最小值为21,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
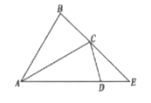
【题目】如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() +bx+c与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,且OC=2OA=2,点D是直线BC下方抛物线上一动点.
+bx+c与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,且OC=2OA=2,点D是直线BC下方抛物线上一动点.
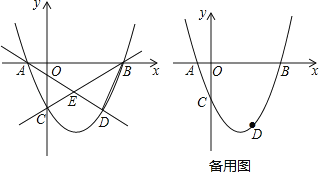
(1)求出抛物线的解析式;
(2)连接AD和BC,AD交BC于点E,当S△ABE:S△BDE=5:4时,求点D的坐标;
(3)点F为y轴上的一点,在(2)的条件下,求DF+![]() OF的最小值.
OF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在推进郑州市城乡生活垃圾分类的行动中,某社区对居民掌握垃圾分类知识的情况进行调査.其中![]() ,
,![]() 两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
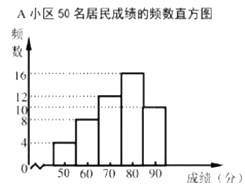
(信息二)上图中,从左往右第四组的成绩如下:
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() ,
,![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 | 40% | 277 | |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数.
小区50名居民成绩的中位数.
(2)请估计![]() 小区1000名居民成绩能超过平均数的人数.
小区1000名居民成绩能超过平均数的人数.
(3)请尽量从多个角度(至少三个),选择合适的统计量分析![]() ,
,![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 分别是某函数图象与
分别是某函数图象与![]() 轴、
轴、![]() 轴的交点,点
轴的交点,点![]() 是此图象上的一动点.设点
是此图象上的一动点.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长为
的长为![]() ,且
,且![]() 与
与![]() 之间满足关系:
之间满足关系:![]() ,则正确结论的序号是( )
,则正确结论的序号是( )
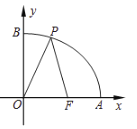
①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() 的最大值是6.
的最大值是6.
A.①②③B.③④C.①②④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,![]() ,AC=3,BC=4.点O为边AB上一点(不与A重合)⊙O是以点O为圆心,AO为半径的圆.当⊙O与三角形边的交点个数为3时,则OA的范围( )
,AC=3,BC=4.点O为边AB上一点(不与A重合)⊙O是以点O为圆心,AO为半径的圆.当⊙O与三角形边的交点个数为3时,则OA的范围( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]() 或
或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com