

分析 (1)根据“共相似点”的定义容易得出结论.
(2)根据题意得:△ABP∽△ACB,由相似三角形的性质得出∠ABP=∠C,同理得:∠CBP=∠A,得出∠ABC=∠A+∠C=180°-∠ABC,求出∠ABC=90°即可;
(3)根据题意得:△PBC∽△CAB,由相似三角形的性质得出∠PBC=∠A,∠PCB=∠ABC,再由角平分线角平分线定义得出∠A=∠ABE=∠PBC,证出△BEC∽△ABC,得出点E是△ABC的边共相似点;由直角三角形的性质得出∠PCB+∠ABC=90°,得出2∠A+2∠A=90°,求出∠A=22.5°;
(4)通过作图得出△ABC的“共相似点”共有8个,根据等边三角形的性质和直角三角形的性质得:顺次连接所有满足条件的P点而围成的多边形的周长为6+$\sqrt{3}$.
解答 解:(1)根据“共相似点”的定义得:等边三角形不存在共相似点.
故答案为:不存在;
(2)△ABC是直角三角形,理由如下:
根据题意得:△ABP∽△ACB,
∴∠ABP=∠C,
同理得:∠CBP=∠A,
∴∠ABC=∠A+∠C=180°-∠ABC,
解得:∠ABC=90°,
∴△ABC是直角三角形;
(3)根据题意得:△PBC∽△CAB,
∴∠PBC=∠A,∠PCB=∠ABC,
∵BE平分∠ABC,
∴∠ABE=∠PBC,
∴∠A=∠ABE=∠PBC,
∴∠PCB=∠ABC=2∠A=2∠PBC,
∵∠BCE=∠ACB,∠PBC=∠A,
∴△BEC∽△ABC,
∴点E是△ABC的边共相似点;
∵CD是△ABC的高,
∴∠CDB=90°,
∴∠PCB+∠ABC=90°,
∴2∠A+2∠A=90°,
解得:∠A=22.5°;
(4)作CP⊥AB于P,则P为△ABC的“共相似点”;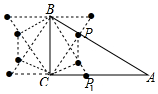
过B作BC的垂线与CP的延长线的交点是△ABC的“共相似点”;
作∠ABC的平分线与AC的交点P1是△ABC的“共相似点”;
过C作BP1的垂线,垂足是△ABC的“共相似点”;
同理:以上四个△ABC的“共相似点”关于直线BC的对称点是△ABC的“共相似点”;
∴△ABC的“共相似点”共有8个,如图所示:
根据等边三角形的性质和直角三角形的性质得:顺次连接所有满足条件的P点而围成的多边形的周长为 2×2+4×$\frac{1}{2}$+2×$\frac{\sqrt{3}}{2}$=6+$\sqrt{3}$;
故答案为:8;6+$\sqrt{3}$.
点评 本题是相似形综合题目,考查了相似三角形的判定与性质、直角三角形的性质等知识;理解“共相似点”定义,证明三角形相似是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:
小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
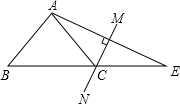 如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )| A. | 45° | B. | 48° | C. | 50° | D. | 72° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com